题目内容
12.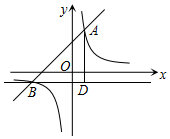 如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(1,3)和B(-3,m).
如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(1,3)和B(-3,m).(1)求一次函数和反比例函数的解析式;
(2)点C是平面直角坐标系内一点,BC∥x轴,AD⊥BC于点D,连结AC,若AC=$\sqrt{5}$CD,求点C的坐标.
分析 (1)把点A的坐标代入反比例函数解析式中,确定出反比例函数的解析式,再把点B的横坐标代入反比例函数解析式中得到点B的坐标,最后把点A和点B的坐标分别代入一次函数解析式中即可确定出一次函数解析式;
(2)由BC∥x轴,AD⊥BC于点D,且A(1,3),B(-3,-1),得出D(1,-1),C(x,-1),CD=|x-1|,AD=4,AC=$\sqrt{5}$CD=$\sqrt{5}$|x-1|.然后在Rt△ACD中利用勾股定理列出方程16+(x-1)2=5(x-1)2,解方程即可.
解答 解:(1)将A(1,3)代入反比例解析式得:k=1×3=3,
则反比例解析式为y=$\frac{3}{x}$,
将B(-3,m)代入反比例解析式得:m=-1,即B(-3,-1).
将A与B坐标代入y=ax+b得:$\left\{\begin{array}{l}{a+b=3}\\{-3a+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$,
则一次函数解析式为y=x+2;
(2)∵BC∥x轴,AD⊥BC于点D,且A(1,3),B(-3,-1),
∴D(1,-1),C(x,-1),
∴CD=|x-1|,AD=4.
∵AC=$\sqrt{5}$CD=$\sqrt{5}$|x-1|,
在Rt△ACD中,∵∠ADC=90°,
∴AD2+CD2=AC2,
即16+(x-1)2=5(x-1)2,
解得x1=3,x2=-1,
∴C点的坐标为(3,-1)或(-1,-1).
点评 此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法求函数解析式,勾股定理,平行于x轴的直线上任意两点的纵坐标相同,熟练掌握待定系数法是解本题的关键.

 阅读快车系列答案
阅读快车系列答案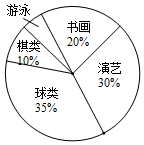 如图是某校参加各兴趣小组的学生人数分布扇形统计图,若参加人数最多的小组是70人,则参加人数最少的小组有( )
如图是某校参加各兴趣小组的学生人数分布扇形统计图,若参加人数最多的小组是70人,则参加人数最少的小组有( )| A. | 5人 | B. | 10人 | C. | 20人 | D. | 40人 |
| A. | (2,-7) | B. | (2,7) | C. | (-2,-7) | D. | (-2,7) |
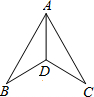 如图,已知∠BAD=∠CAD,图中再补充一个条件后不能说明△ABD≌△ACD,则这个条件是( )
如图,已知∠BAD=∠CAD,图中再补充一个条件后不能说明△ABD≌△ACD,则这个条件是( )| A. | AB=AC | B. | ∠B=∠C | C. | BD=CD | D. | ∠ADB=∠ADC |
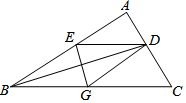 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.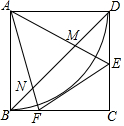 如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④$\widehat{BD}$与EF相切;⑤EF∥MN.其中正确结论的个数是( )
如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④$\widehat{BD}$与EF相切;⑤EF∥MN.其中正确结论的个数是( ) 在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-1与x轴交于A,B两点(点A在点B左侧)
在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-1与x轴交于A,B两点(点A在点B左侧)