题目内容
已知m、n为整数,3m+2=5n+3,且3m+9>30,5n+3<40,则mn的值是 ________
84
分析:由已知3m+2=5n+3,且3m+9>30,5n+3<40,分别求出m.n的取值范围,再根据已知分析得出符合要求的值,从而求出答案.
解答:∵5n+3<40,3m+2=5n+3,
∴3m+2<40,∴m< ,
,
∵3m+9>30,∴m>7,
∴7<m< ,
,
∴符合要求的答案有:8,9,10,11,12;
∵3m+9>30,
∴3m+2>23,
∵3m+2=5n+3,
5n+3>23,
∴n>4,
∵5n+3<40,
∴n<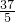 ,
,
∴符合要求的答案有:5,6,7;
∵3m+2=5n+3,
∴当n=5时,3m+2=5×5+3,
∴m= (不合题意舍去),
(不合题意舍去),
∴当n=6时,3m+2=6×5+3,
∴m=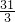 (不合题意舍去),
(不合题意舍去),
∴当n=7时,3m+2=5×7+3,
∴m=12,
故只有n=7,m=12符合要求,
∴nm=84.
故答案为:84.
点评:此题考查的是一元一次不等式组的解法和一元一次方程的解,题目综合性较强,根据题意分别对m,n进行分析是解决问题的关键.
分析:由已知3m+2=5n+3,且3m+9>30,5n+3<40,分别求出m.n的取值范围,再根据已知分析得出符合要求的值,从而求出答案.
解答:∵5n+3<40,3m+2=5n+3,
∴3m+2<40,∴m<
 ,
,∵3m+9>30,∴m>7,
∴7<m<
 ,
,∴符合要求的答案有:8,9,10,11,12;
∵3m+9>30,
∴3m+2>23,
∵3m+2=5n+3,
5n+3>23,
∴n>4,
∵5n+3<40,
∴n<
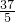 ,
,∴符合要求的答案有:5,6,7;
∵3m+2=5n+3,
∴当n=5时,3m+2=5×5+3,
∴m=
 (不合题意舍去),
(不合题意舍去),∴当n=6时,3m+2=6×5+3,
∴m=
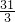 (不合题意舍去),
(不合题意舍去),∴当n=7时,3m+2=5×7+3,
∴m=12,
故只有n=7,m=12符合要求,
∴nm=84.
故答案为:84.
点评:此题考查的是一元一次不等式组的解法和一元一次方程的解,题目综合性较强,根据题意分别对m,n进行分析是解决问题的关键.

练习册系列答案
相关题目