题目内容
4.某商扬准备进行装修,请甲、乙两个装修队.若两队同时施工,则8天完成,需付两队费用共3520元:若甲队先单独做6天,则乙队单独再做12天可以完成任务,需付两队费用共3480元.(1)甲、乙两队工作一天,商场各应付多少元?
(2)单独请哪个队装修,商场所付费用最少?
分析 (1)设甲每天费用为x元,乙每天费用为y元,根据题意可得等量关系:①甲、乙两个工程队同时施工,8天可以完成,需付两队费用共3520元;②甲队单独做6天,再请乙队单独做12天可以完成,需付两队费用共3480元,根据费用列出方程组,解方程组即可;
(2)设甲每天完成x,乙每天完成y,根据题意可得等量关系:①甲和乙8天的工作量=1,②甲6天的工作量+乙12天的工作量=1,根据等量关系列出方程组,再解可得甲和乙的工作效率,再求费用即可.
解答 解:(1)设甲每天费用为x元,乙每天费用为y元,由题意得:
$\left\{\begin{array}{l}{8x+8y=3520}\\{6x+12y=3480}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=300}\\{y=140}\end{array}\right.$.
答:甲每天的费用为300元,乙每天的费用为140元.
(2)设甲每天完成x,乙每天完成y,由题意得:
$\left\{\begin{array}{l}{8x+8y=1}\\{6x+12y=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{1}{12}}\\{y=\frac{1}{24}}\end{array}\right.$,
甲单独做需要12天完成,乙单独做需要24天完成.
甲单独做需要12×300=3600元,乙单独做需要24×140=3360元.
答:乙队单独完成费用较少.
点评 此题主要考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,列出方程组.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.我国“天河二号”计算机的运算速度世界最快,若完成一次基本运算的时间约为0.000000000001s,把这个数0.000000000001用科学记数法可表示为( )
| A. | 0.1×10-11 | B. | 1×10-12 | C. | 1×10-11 | D. | 0.1×10-12 |
16.杭州丝绸历史悠久,质地轻软,色彩绮丽,早在汉代,就已通过“丝绸之路”远销国外,小丽在网上开设杭州丝绸专卖店,专卖丝巾、旗袍等,一次,小丽发现一张进货单上的一个信息是:A款丝巾的进货单价比B款丝巾多40元,花960元购进A款丝巾的数量与花720元购进B款丝巾的数量相同.
(1)问:A,B款丝巾的进货单价分别是多少元?
(2)小丽在销售单上记录了两天的数据,如下表所示:
问:两款丝巾的销售单价分别是多少?
(3)根据(1)(2)所给的信息,小丽要花费1400元购进A,B两款丝巾若干条,问:有哪几种进货方案?根据计算说明哪种进货方案的总利润做高.
(1)问:A,B款丝巾的进货单价分别是多少元?
(2)小丽在销售单上记录了两天的数据,如下表所示:
| 日期 | A款丝巾(条) | B款丝巾(条) | 销售总额(元) |
| 6月10日 | 4 | 6 | 2160 |
| 6月11日 | 6 | 8 | 3040 |
(3)根据(1)(2)所给的信息,小丽要花费1400元购进A,B两款丝巾若干条,问:有哪几种进货方案?根据计算说明哪种进货方案的总利润做高.
14.为庆祝抗战胜利70周年,我市某楼盘让利于民,决定将原价为每平方米c元的商品房价降价10%销售,降价后的销售价为每平方米( )元.
| A. | c-10% | B. | 10%c | C. | (1-10%)c | D. | (1+10%)c |
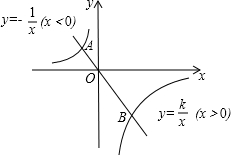 如图,在平面直角坐标系中,过原点的一条直线分别与反比例函数y=-$\frac{1}{x}$(x<0)和反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,且OB=2OA,则k的值为-4.
如图,在平面直角坐标系中,过原点的一条直线分别与反比例函数y=-$\frac{1}{x}$(x<0)和反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,且OB=2OA,则k的值为-4. 如图,矩形ABCD中,AB=4,AD=6,点E在边AD上,且AE:ED=1:2.动点P 从点A 出发,沿AB 运动到点B 停止.过点E作EF⊥PE交射线BC于点F.设点M是线段EF的中点,则在点P运动的整个过程中,点M的运动路径长为4.
如图,矩形ABCD中,AB=4,AD=6,点E在边AD上,且AE:ED=1:2.动点P 从点A 出发,沿AB 运动到点B 停止.过点E作EF⊥PE交射线BC于点F.设点M是线段EF的中点,则在点P运动的整个过程中,点M的运动路径长为4.