题目内容
16.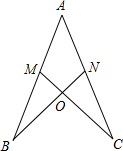 已知:如图,M、N分别在AB和AC上,CM与BN相交于点O,若BM=CN,∠B=∠C.求证:AB=AC.
已知:如图,M、N分别在AB和AC上,CM与BN相交于点O,若BM=CN,∠B=∠C.求证:AB=AC.
分析 根据全等三角形判定得出△BOM≌△CON,得出BO=CO,OM=ON,得出BM=BN,再证明出△ABN≌△ACM,得出AB=AC.
解答 证明:在△BOM和△CON中,
$\left\{\begin{array}{l}{∠BOM=∠CON}\\{∠B=∠C}\\{BM=CN}\end{array}\right.$,
∴△BOM≌△CON(AAS),
∴BO=CO,OM=ON,
∴BN=CM,
在△ABN和△ACM中,
$\left\{\begin{array}{l}{∠B=∠C}\\{∠A=∠A}\\{BN=CM}\end{array}\right.$,
∴△ABN≌△ACM(AAS),
∴AB=AC.
点评 本题考查全等三角形的判定与性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
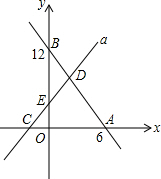 如图,直线m为y=x+3,且直线a与x轴交于点C,直线b经过A、B两点,两直线相交于点D.
如图,直线m为y=x+3,且直线a与x轴交于点C,直线b经过A、B两点,两直线相交于点D.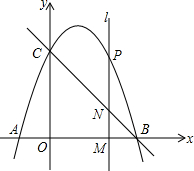 如图,直线BC交x轴、y轴于点B(3,0)和C(0,3),且抛物线y=-x2+bx+c过B、C两点,与x轴交于另一点A.
如图,直线BC交x轴、y轴于点B(3,0)和C(0,3),且抛物线y=-x2+bx+c过B、C两点,与x轴交于另一点A.