题目内容
【题目】阅读材料:已知方程![]() ,
,![]() 且
且![]() ,求
,求![]() 的值.
的值.
解:由![]() ,及
,及![]() ,可知
,可知![]() ,
,![]() .
.
又![]()
![]() ,
,
![]() .
.
![]()
![]() 可变形为
可变形为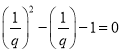 ,
,
根据![]() 和
和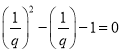 的特征.
的特征.
![]() 、
、![]() 是方程
是方程![]() 的两个不相等的实数根,
的两个不相等的实数根,
则![]() ,即
,即![]() .
.
根据阅读材料所提供的方法,完成下面的解答.
已知:![]() ,
,![]() 且
且![]() ,
,
(1)求:![]() 的值.
的值.
(2)求:![]() .
.
【答案】(1)![]() ;(2)29.
;(2)29.
【解析】
由![]() -2=0得到2n2-5n-1=0,根据题目所给的方法得到m、n是方程2x2-5x-1=0的两个不相等的实数根,根据根与系数的关系得到m+n=
-2=0得到2n2-5n-1=0,根据题目所给的方法得到m、n是方程2x2-5x-1=0的两个不相等的实数根,根据根与系数的关系得到m+n=![]() ,mn=
,mn=![]() .
.
(1)根据根与系数的关系得到mn=![]() ,即可解答;
,即可解答;
(2)利用分式的运算法则对所求式子变形,然后利用整体代入的方法计算.
∵![]() -2=0,
-2=0,
∴2n2-5n-1=0,
根据2m2-5m-1=0和2n2-5n-1=0的特征,
∴m、n是方程2x2-5x-1=0的两个不相等的实数根,
∴m+n=![]() ,mn=
,mn=![]() ,
,
(1)mn=![]() ;
;
(2)![]() =
=![]()
 29.
29.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
【题目】探究函数![]() 的图象与性质.
的图象与性质.
小娜根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小娜的探究过程,请补充完整:
的图象与性质进行了探究.下面是小娜的探究过程,请补充完整:
(1)下表是x与y的几组对应值.
x | … |
|
| 0 |
| 2 |
| 3 | … |
y | … |
|
| 0 | m | n |
| 3 | … |
请直接写出:m= ,n= ;
(2)如图,小娜在平面直角坐标系xOy中,描出了上表中已经给出的各组对应值为坐标的点,请再描出剩下的两个点,并画出该函数的图象;

(3)结合画出的函数图象,解决问题:若方程![]() 有三个不同的解,记为x1, x2, x3,且x1< x2<x3. 请直接写出x1+ x2+x3的取值范围.
有三个不同的解,记为x1, x2, x3,且x1< x2<x3. 请直接写出x1+ x2+x3的取值范围.