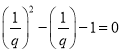��Ŀ����
����Ŀ��̽������![]() ��ͼ�������ʣ�
��ͼ�������ʣ�
С�ȸ���ѧϰ�����ľ��飬�Ժ���![]() ��ͼ�������ʽ�����̽����������С�ȵ�̽�����̣��벹��������
��ͼ�������ʽ�����̽����������С�ȵ�̽�����̣��벹��������
��1���±���x��y�ļ����Ӧֵ��
x | �� |
|
| 0 |
| 2 |
| 3 | �� |
y | �� |
|
| 0 | m | n |
| 3 | �� |
��ֱ��д����m= ��n= ��
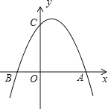
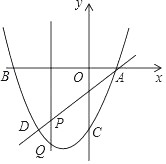
��2����ͼ��С����ƽ��ֱ������ϵxOy�У�������ϱ����Ѿ������ĸ����ӦֵΪ����ĵ㣬�������ʣ�µ������㣬�������ú�����ͼ��

��3����ϻ����ĺ���ͼ������⣺������![]() ��������ͬ�Ľ⣬��Ϊx1, x2, x3����x1< x2<x3. ��ֱ��д��x1+ x2+x3��ȡֵ��Χ.
��������ͬ�Ľ⣬��Ϊx1, x2, x3����x1< x2<x3. ��ֱ��д��x1+ x2+x3��ȡֵ��Χ.
���𰸡���1��m=1��n=0��
��2����������
��3��![]()
��������
��1����x=1���룬�����m��ֵ����x=2���룬�����n��ֵ
��2������㣬�����Ӽ��ɣ�
��3��y=a��![]() ����ͼ��Ľ�������꼴��x1��x2��x3��ֵ��
����ͼ��Ľ�������꼴��x1��x2��x3��ֵ��
��x1< x2<x3, ��ͼ�۲�ɵ�0<x1<1, 1<x2<2, 2<x3<1+![]() ,
,
����![]()
�⣺��1��m=1��n=0��
��2����ͼ��

��3����y=a��![]() ����ͼ��Ľ�������꼴��x1��x2��x3��ֵ��
����ͼ��Ľ�������꼴��x1��x2��x3��ֵ��
��x1< x2<x3.
��ͼ�۲�ɵ�0<x1<1, 1<x2<2, 2<x3<1+![]() ,
,
��![]()

��ϰ��ϵ�д�
 ������ϵ�д�
������ϵ�д�
�����Ŀ