题目内容
【题目】如图，在平面直角坐标系中，二次函数
的图象与x轴交于A、B两点，B点的坐标为(3，0)，与y轴交于点C（0，－3），点P是直线BC下方抛物线上的一个动点．
（1）求二次函数解析式；
（2）连接PO，PC，并将△POC沿y轴对折，得到四边形
.是否存在点P，使四边形
为菱形？若存在，求出此时点P的坐标；若不存在，请说明理由；
（3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积.
【答案】解：（1）将B、C两点的坐标代入
，得
， 解得
。
∴二次函数的解析式为
。
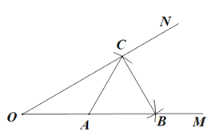
（2）存在。如图1，假设抛物线上存在点P，使四边形
为菱形，连接
交CO于点E。
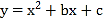
∵四边形
为菱形， K∴PC=PO，且PE⊥CO。
∴OE=EC=
，即P点的纵坐标为
。
由
解得：
（不合题意，舍去）。
∴存在这样的点，此时P点的坐标为（
，
）。
（3）如图2，连接PO，作PM⊥x于M，PN⊥y于N。设P点坐标为（x，
），
由
=0，得点A坐标为（－1，0）。
∴AO=1，OC=3， OB=3，PＭ=
，PN＝x。
∴S四边形ABPC=
+
+
=
AO·OC+
OB·PM+
OC·PN
=
×1×3+
×3×(
)+
×3×x
=
=
。
∴当x=
时，四边形ABPC的面积最大．此时P点坐标为（
，
），四边形ABPC的最大面积为
。
【解析】
试题（1）直接把B（3，0）、C（0，－3）代入可得到关于b、c的方程组，解方程组求得b，c，则从而求得二次函数的解析式。
（2）假设抛物线上存在点P，使四边形
为菱形，连接
交CO于点E，则PO=PC，根据翻折的性质得OP′=OP，CP′=CP，易得四边形POP′C为菱形，又E点坐标为（0，
），则点P的纵坐标为
，把y=
代入
可求出对应x的值，然后确定满足条件的P点坐标。
（3）由S四边形ABPC=++求出S四边形ABPC关于P点横坐标的函数表达式，应用二次函数的最值原理求解。
