题目内容
8．若-2x2+5x-2＞0，则$\sqrt{4{x}^{2}-4x+1}$+2|x-2|等于3．分析 首先解不等式求得x的范围，然后利用二次根式的性质以及绝对值的性质即可化简求值．
解答 解：解方程-2x2+5x-2=0得x=$\frac{1}{2}$或2．
则不等式-2x2+5x-2＞0的解集是：$\frac{1}{2}$＜x＜2．
则2x-1＞0，x-2＜0．
则原式=$\sqrt{（2x-1）^{2}}$+2|x-2|
=|2x-1|+2|x-2|
=2x-1+2（2-x）
=3．
故答案是：3．
点评 本题考查了二次根式的化简以及绝对值的性质、不等式的解法，正确求得x的范围是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，各边都相等的五边形ABCDE中，∠ABC=2∠DBE，求∠ABC．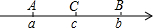
如图，已知数轴上点A，B，C所对应的数a，b，c都不为0，且C是AB的中点，如果|a+b|-|a-2c|+|b-2c|-|a+b-2c|=0，试确定原点O的大致位置．
如图，边长为m，n的长方形，它的周长为10，面积为6，则m2n+mn2的值为30．
18．如果x2-x+2的值为7，则-$\frac{1}{2}$x2+$\frac{1}{2}$x+5的值为（ ）
| A． | $\frac{5}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{15}{2}$ | D． | 答案不唯一 |