题目内容
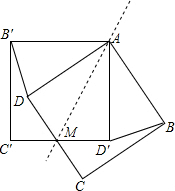 如图,M为线段CD上的一个动点(不与C、D重合),正方形ABCD与正方形AB′C′D′关于直线AM成轴对称,
如图,M为线段CD上的一个动点(不与C、D重合),正方形ABCD与正方形AB′C′D′关于直线AM成轴对称,(1)若∠DAM=x°,∠CMD′=y°,求y与x的关系式;
(2)请你探索线段B′D和BD′的关系,并说明你的理由.
考点:正方形的性质,轴对称的性质
专题:
分析:(1)根据直角三角形两锐角互余表示出∠AMD,再根据轴对称的性质可得∠AMD′=∠AMD,然后根据平角等于180°列式整理即可得解;
(2)根据正方形的性质可得AB=AD,AB′=AD′,∠BAD=∠B′AD′=90°,根据同角的余角相等求出∠BAD′=∠B′AD,然后利用“边角边”证明△ABD′和△ADB′全等,根据全等三角形对应边相等可得B′D=BD′.
(2)根据正方形的性质可得AB=AD,AB′=AD′,∠BAD=∠B′AD′=90°,根据同角的余角相等求出∠BAD′=∠B′AD,然后利用“边角边”证明△ABD′和△ADB′全等,根据全等三角形对应边相等可得B′D=BD′.
解答:解:(1)∵四边形ABCD是正方形,
∴∠ADC=90°,
∴∠AMD=90°-∠DAM=90°-x°,
由轴对称的性质得,∠AMD′=∠AMD=90°-x°,
∵∠AMD′+∠AMD+∠CMD′=180°,
∴90°-x°+90°-x°+y°=180°,
∴y=2x;
(2)B′D=BD′.
证明如下:在正方形ABCD与正方形AB′C′D′中,AB=AD,AB′=AD′,∠BAD=∠B′AD′=90°,
∵∠BAD′+∠DAD′=∠B′AD+∠DAD′=90°,
∴∠BAD′=∠B′AD,
在△ABD′和△ADB′中,
,
∴△ABD′≌△ADB′(SAS),
∴B′D=BD′.
∴∠ADC=90°,
∴∠AMD=90°-∠DAM=90°-x°,
由轴对称的性质得,∠AMD′=∠AMD=90°-x°,
∵∠AMD′+∠AMD+∠CMD′=180°,
∴90°-x°+90°-x°+y°=180°,
∴y=2x;
(2)B′D=BD′.
证明如下:在正方形ABCD与正方形AB′C′D′中,AB=AD,AB′=AD′,∠BAD=∠B′AD′=90°,
∵∠BAD′+∠DAD′=∠B′AD+∠DAD′=90°,
∴∠BAD′=∠B′AD,
在△ABD′和△ADB′中,
|
∴△ABD′≌△ADB′(SAS),
∴B′D=BD′.
点评:本题考查了正方形的性质,轴对称的性质,全等三角形的判定与性质,熟记各性质并确定出全等三角形和全等的条件是解题的关键.

练习册系列答案
相关题目
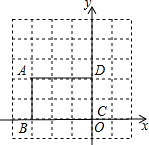 已知如图,以长方形ABCD的顶点C为坐标原点,BC边、CD边所在直线为坐标轴建立直角坐标系,则图中,点A的坐标是( )
已知如图,以长方形ABCD的顶点C为坐标原点,BC边、CD边所在直线为坐标轴建立直角坐标系,则图中,点A的坐标是( )| A、(2,3) |
| B、(-2,3) |
| C、(-3,2) |
| D、(-2,-3) |
 在正方形ABCD的外侧,作等边△ADE,设BE与AD交于点F,当AF=1时,求DF的长.
在正方形ABCD的外侧,作等边△ADE,设BE与AD交于点F,当AF=1时,求DF的长.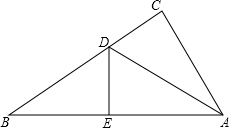 如图,Rt△ABC中,∠C=90°,AB=13,AC=5,AD平分∠CAB,DE⊥AB于E,
如图,Rt△ABC中,∠C=90°,AB=13,AC=5,AD平分∠CAB,DE⊥AB于E,