Question

在正方形ABCD的外侧，作等边△ADE，设BE与AD交于点F，当AF=1时，求DF的长．

Answer 1

考点：正方形的性质,相似三角形的判定与性质

专题：

分析：过点E作EH⊥AD于H，根据等边三角形的性质可得AH=DH，再求出

EH

AE

，再求出AB∥EH，然后判断出△ABF和△HEF相似，根据相似三角形对应边成比例求出

FH

AF

=

EH

AB

，然后求出FH，再求出AH，然后根据DF=DH+FH计算即可得解．

解答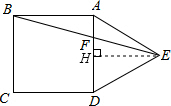：解：如图，过点E作EH⊥AD于H，
∵△ADE是等边三角形，
∴AH=DH，

EH

AE

=

3

2

，
∵∠BAD=90°，
∴∠BAD=∠AHE，
∴AB∥EH，
∴△ABF∽△HEF，
∴

FH

AF

=

EH

AB

，
∵AF=1，AB=AE，
∴FH=1×

3

2

=

3

2

，
∴AH=AF+FH=1+

3

2

，
∵AH=DH=1+

3

2

，
∴DF=FH+DH=

3

2

+1+

3

2

=1+

3

．

点评：本题考查了正方形的性质，相似三角形的判定与性质，等边三角形的性质，作辅助线构造出相似三角形是解题的关键．