题目内容
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,E为CD中点,已知AB=5,BE=6.5,求梯形的面积.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,E为CD中点,已知AB=5,BE=6.5,求梯形的面积.考点:直角梯形
专题:
分析:首先过点E作EF∥BC于点F,进而得出EF是原梯形的中位线,进而得出梯形面积.
解答: 解:过点E作EF∥BC于点F,
解:过点E作EF∥BC于点F,
∵AD∥BC,AB⊥BC,E为CD中点,
∴EF是梯形ABCD的中位线,EF⊥AB,
∵AB=5,BE=6.5,
∴BF=2.5,
则EF=
=
=6,
∴梯形的面积为:
×2EF×AB=EF×AB=6×5=30.
 解:过点E作EF∥BC于点F,
解:过点E作EF∥BC于点F,∵AD∥BC,AB⊥BC,E为CD中点,
∴EF是梯形ABCD的中位线,EF⊥AB,
∵AB=5,BE=6.5,
∴BF=2.5,
则EF=
| BE2-BF2 |
| 6.52-2.52 |
∴梯形的面积为:
| 1 |
| 2 |
点评:此题主要考查了直角梯形的性质,得出梯形中位线EF的长是解题关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
数轴上到-2点距离为3的点所表示的数是( )
| A、1或-5 | B、-5 |
| C、1 | D、以上都不对 |
 如图,△ABC中,AD⊥BC于D,BF=AC,FD=CD.求证:AC⊥BE.
如图,△ABC中,AD⊥BC于D,BF=AC,FD=CD.求证:AC⊥BE.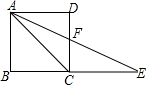 如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:①∠E=22.5°; ②∠AFC=112.5°; ③∠ACE=135°;④AC=CE;⑤AD:CE=1:2.其中正确的有
如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:①∠E=22.5°; ②∠AFC=112.5°; ③∠ACE=135°;④AC=CE;⑤AD:CE=1:2.其中正确的有 如图,在正方形ABCD中,E为BC上的点,F为CD边上的点,且AE=AF,AB=4,设EC=x,△AEF的面积为y,则y与x之间的函数关系式是
如图,在正方形ABCD中,E为BC上的点,F为CD边上的点,且AE=AF,AB=4,设EC=x,△AEF的面积为y,则y与x之间的函数关系式是