题目内容
13.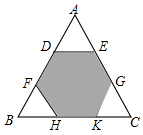 如图,正三角形的边长为12cm,剪去三个角后成为一个正六边形,则这个正六边形的内部任意一点到各边的距离和为12$\sqrt{3}$cm.
如图,正三角形的边长为12cm,剪去三个角后成为一个正六边形,则这个正六边形的内部任意一点到各边的距离和为12$\sqrt{3}$cm.
分析 作ON⊥BC于N,根据正三角形和正六边形的性质求出正六边形DFHKGE的面积,根据三角形的面积公式计算即可.
解答 解:作ON⊥BC于N,
∵六边形DFHKGE是正六边形,
∴AD=DE=DF=BF=4,
∴ OH=4,
OH=4,
由勾股定理得,ON=$\sqrt{O{H}^{2}-H{N}^{2}}$=2$\sqrt{3}$,
则正六边形DFHKGE的面积=$\frac{1}{2}$×4×2$\sqrt{3}$×6=24$\sqrt{3}$,
设这个正六边形的内部任意一点到各边的距离和为h,
则$\frac{1}{2}$×4×h=24$\sqrt{3}$,
解得,h=12$\sqrt{3}$,
故答案为:12$\sqrt{3}$.
点评 本题考查的是正多边形和圆的知识,掌握正三角形的性质、正六边形的中心角的计算公式是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
4.已知$\frac{1}{a}$-$\frac{1}{b}$=$\frac{1}{2}$,则$\frac{ab}{a-b}$的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | -2 | D. | 2 |
1.下列统计中,适合用全面调查的是( )
| A. | 检测矿区的空气质量 | |
| B. | 审查某篇文章中的错别字 | |
| C. | 调查全国七年级学生视力状况 | |
| D. | 调查山东电视台“我是大明星”的收视率 |
2.一粒花粉的质量约为0.000037毫克,那么0.000037可用科学记数法表示为( )
| A. | 3.7×10-5 | B. | 3.7×10-6 | C. | 37×10-7 | D. | 3.7×10-8 |
 如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=70°,则∠BCE的度数为70°.
如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=70°,则∠BCE的度数为70°. 如图,在Rt△ACB中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在边BA上以2cm/s的速度向点A匀速运动,同时动点N从点C出发,在边CB上以$\sqrt{3}$cm/s的速度向点B匀速运动,设运动时间为t s(0≤t≤5),连接MN.
如图,在Rt△ACB中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在边BA上以2cm/s的速度向点A匀速运动,同时动点N从点C出发,在边CB上以$\sqrt{3}$cm/s的速度向点B匀速运动,设运动时间为t s(0≤t≤5),连接MN.