题目内容
如图,在△ABC中,∠ABC=∠ACB,BO平分∠ABC,CO平分∠ACB.
(1)想想看,你能得到什么结论?
(2)若过点O作一直线EF和边BC平行,与AB交于点E,与AC交于点F.则图(2)中有几个等腰三角形?线段EF和EB、FC之间有怎样的关系?
(3)若∠ABC≠∠ACB,其他条件不变,图(3)中是否还有等腰三角形?(2)中第二问的关系是否还存在?写出你的理由.
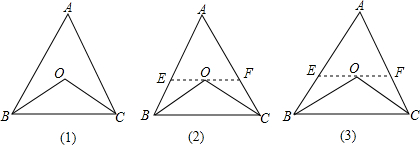
(1)想想看,你能得到什么结论?
(2)若过点O作一直线EF和边BC平行,与AB交于点E,与AC交于点F.则图(2)中有几个等腰三角形?线段EF和EB、FC之间有怎样的关系?
(3)若∠ABC≠∠ACB,其他条件不变,图(3)中是否还有等腰三角形?(2)中第二问的关系是否还存在?写出你的理由.

考点:等腰三角形的判定与性质,平行线的性质
专题:探究型
分析:(1)由条件可得到∠OBC=∠OCB,可得到OB=OC;
(2)由平行和角平分线可得到∠EBO=∠EOB,可得到OE=BE,同理OF=CF,则AE=AF,结合(1)OB=OC,所以共有5个等腰三角形,可得到EF=BE+FC;
(3)同(2)可得EO=EB,FO=FC,所以存在等腰三角形,关系仍然存在.
(2)由平行和角平分线可得到∠EBO=∠EOB,可得到OE=BE,同理OF=CF,则AE=AF,结合(1)OB=OC,所以共有5个等腰三角形,可得到EF=BE+FC;
(3)同(2)可得EO=EB,FO=FC,所以存在等腰三角形,关系仍然存在.
解答:解:(1)可得结论OB=OC,△OBC为等腰三角形,
∵∠ABC=∠ACB,BO平分∠ABC,CO平分∠ACB,
∴∠OBC=∠OCB,
∴OB=OC,
∴△OBC为等腰三角形;
(2)∵BO平分∠ABC,
∴∠EBO=∠CBO,
∵EF∥BC,
∴∠CBO=∠EOB,
∴∠EBO=∠EOB,
∴EO=EB,
∴△EOB为等腰三角形,
同理可得FO=FC,
∴△FOC为等腰三角形,
∵∠ABC=∠ACB,
∴AB=AC,
∴△ABC为等腰三角形,
∵EF∥BC,
∴∠AEF=∠ABC=∠ACB=∠AFE,
∴AE=AF,
∴△AEF为等腰三角形,
由(1)可知OB=OC,
∴△OBC为等腰三角形,
综上可知有五个等腰三角形,
∵EO=BE,OF=CF,
∴EF=EO+OF=BE+CF;
(3)有等腰三角形,关系式仍然存在,
同(2)可知BE=OE,CF=OF,
∴△BEO和△CFO为等腰三角形,
EF=BE+CF.
∵∠ABC=∠ACB,BO平分∠ABC,CO平分∠ACB,
∴∠OBC=∠OCB,
∴OB=OC,
∴△OBC为等腰三角形;
(2)∵BO平分∠ABC,
∴∠EBO=∠CBO,
∵EF∥BC,
∴∠CBO=∠EOB,
∴∠EBO=∠EOB,
∴EO=EB,
∴△EOB为等腰三角形,
同理可得FO=FC,
∴△FOC为等腰三角形,
∵∠ABC=∠ACB,
∴AB=AC,
∴△ABC为等腰三角形,
∵EF∥BC,
∴∠AEF=∠ABC=∠ACB=∠AFE,
∴AE=AF,
∴△AEF为等腰三角形,
由(1)可知OB=OC,
∴△OBC为等腰三角形,
综上可知有五个等腰三角形,
∵EO=BE,OF=CF,
∴EF=EO+OF=BE+CF;
(3)有等腰三角形,关系式仍然存在,
同(2)可知BE=OE,CF=OF,
∴△BEO和△CFO为等腰三角形,
EF=BE+CF.
点评:本题主要考查等腰三角形的判定和性质,注意利用平行线的性质和角平分线的定义得到角相等是解题的关键.

练习册系列答案
相关题目
代数式3x2y-4x3y2-5xy3-1按x的升幂排列,正确的是( )
| A、-4x3y2+3x2y-5xy3-1 |
| B、-5xy3+3x2y-4x3y2-1 |
| C、-1+3x2y-4x3y2-5xy3 |
| D、-1-5xy3+3x2y-4x3y2 |
 如图,在△ABC中,AC=6,AB=9,BC=14,AB、AC的垂直平分线分别交BC于点F、E,求△EAF的周长.
如图,在△ABC中,AC=6,AB=9,BC=14,AB、AC的垂直平分线分别交BC于点F、E,求△EAF的周长.