题目内容
14．
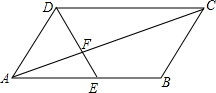如图，在?ABCD中，AE：AB=1：2．（1）求△AEF与△CDF的周长的比；
（2）若S△AEF=8cm2，求S△CDF，S?ABCD．
分析 （1）根据平行四边形的对边平行且相等可得AB∥DC，AB=DC，然后求出△AEF和△CDF相似，根据相似三角形周长的比等于相似比可得周长之比等于AE：CD，再根据AE：AB=1：2．求出AE：CD，从而得解；
（2）根据相似三角形面积的比等于相似比的平方列式计算即可得解．
解答 解：（1）∵四边形ABCD是平行四边形，
∴AB∥DC，AB=DC，
∴△AEF∽△CDF，
∴C△AEF：C△CDF=AE：CD=AE：AB，
∵AE：AB=1：2，
∴AE：CD=1：2，
∴C△AEF：C△CDF=1：2；
（2）∵△AEF∽△CDF，
∴S△AEF：S△CDF=1：4，
∵S△AEF=8cm2，
∴S△CDF=32cm2，
S△ADF=2S△AEF=16，
∴S?ABCD．=2S△ACD=2（S△ADF+S△CDF）=96cm2．
点评 本题考查了相似三角形的判定与性质，平行四边形的性质，由平行线判定相似三角形是最常用的方法，还利用了相似三角形周长的比等于对应边的比，面积的比等于相似比的平方的性质，熟记性质是解题的关键．
练习册系列答案
黄冈创优卷系列答案
相关题目
2．数轴上到-1的距离等于2的点所表示的数是（ ）
| A． | ±2 | B． | ±3 | C． | 2 | D． | -3或1 |
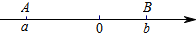阅读材料：我们知道，若点A、B在数轴上分别表示 有理数a、b（如图所示），A、B两点间的距离表示为AB，则AB=|a-b|．所以式子|x-2|的几何意义是数轴上表示x的点与表示2的点之间的距离．根据上述材料，解答下列问题：
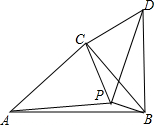如图，在△ABC中，∠ACB=90°，AC=BC，P是△ABC内的一点且PA=3，PB=1，PC=CD=2，CD⊥PC．