题目内容
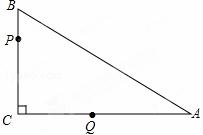
如图,在△ABC中,∠C=90°,BC=3,AB=5.点P从点B出发,以每秒1个单位长度沿B→C→A→B的方向运动;点Q从点C出发,以每秒 2个单位沿C→A→B方向的运动,到达点B后立即原速返回,若P、Q两点同时运动,相遇后同时停止,设运动时间为t秒.
2个单位沿C→A→B方向的运动,到达点B后立即原速返回,若P、Q两点同时运动,相遇后同时停止,设运动时间为t秒.
(1)当t= 时,点P与点Q相遇;
(2)在点P从点B到点C的运动过程中,当ι为何值时,△PCQ为等腰三角形?
(3)在点Q从点B返回点A的运动过程中,设△PCQ的面积为s平方单位.求s与ι之间的函数关系式;
|
解:(1)7
(2)Q从C到A的时间是2秒,P从A到C的时间是3秒.
则当0≤t≤2时,若△PCQ为等腰三角形,则一定有:PC=CQ,
即3﹣t=2t,解得:t=1
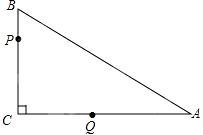
当2<t≤3时,若△PCQ为等腰三角形,则一定有PQ=QC(如图1).则Q在PC的中垂线上,作QH⊥AC,则QH=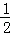 PC.△AQH∽△ABC,
PC.△AQH∽△ABC,
 在直角△AQH中,AQ=2t﹣4,则QH=
在直角△AQH中,AQ=2t﹣4,则QH=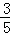 AQ=
AQ=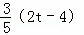
∵PC=BC﹣BP=3﹣t,
∴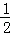 ×
×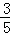 (2t﹣4)=3﹣t,
(2t﹣4)=3﹣t,
解得:t=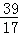 ;
;
综上:当t=1或t=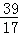 时△PCQ为等腰三角形-
时△PCQ为等腰三角形-
(3)在点Q从点B返回点A的运动过程中,P一定在AC上,则PC=t﹣3,BQ=2t﹣9,
即AQ=5﹣(2t﹣9)=14﹣2t.
同(2)可得:△PCQ中,PC边上的高是: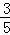 (14﹣2t),
(14﹣2t),
故s=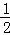 (t﹣3)×
(t﹣3)×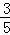 (14﹣2t)=
(14﹣2t)=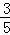 (﹣t2+10t﹣21).
(﹣t2+10t﹣21).

练习册系列答案
相关题目

 是同类二次根式的是( )
是同类二次根式的是( )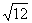 B.
B.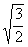 C.
C. D.
D.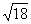
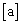 表示不超过a的最大整数,如
表示不超过a的最大整数,如 ,现对72进行如下操作:
,现对72进行如下操作: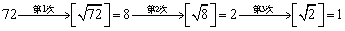 ,
, )
)
 +3x-1=0的根可视为函数y=x+3的图象与函数y=
+3x-1=0的根可视为函数y=x+3的图象与函数y= 的图象交点的横坐标,则方程x
的图象交点的横坐标,则方程x +2x-1=0的实根x
+2x-1=0的实根x 所在的范围是( )
所在的范围是( ) B.
B. C.
C. D.
D.