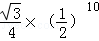题目内容
 小明作出了边长为2的第1个正△A1B1C1,算出了正△A1B1C1的面积.然后分别取△A1B1C1的三边中点A2、B2、C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积.用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第10个正△A10B10C10的面积是
小明作出了边长为2的第1个正△A1B1C1,算出了正△A1B1C1的面积.然后分别取△A1B1C1的三边中点A2、B2、C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积.用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第10个正△A10B10C10的面积是
| ||
| 49 |
| ||
| 49 |
分析:根据相似三角形的性质,先求出正△A2B2C2,正△A3B3C3的面积,依此类推△AnBnCn的面积是
,从而求出第10个正△A10B10C10的面积.
| ||
| 4n-1 |
解答:解:正△A1B1C1的面积是
×22=
=
,
∵△A2B2C2与△A1B1C1相似,并且相似比是1:2,
∴面积的比是1:4,
则正△A2B2C2的面积是
×
=
=
;
∵正△A3B3C3与正△A2B2C2的面积的比也是1:4,
∴面积是
×
=
=
;
依此类推△AnBnCn与△An-1Bn-1Cn-1的面积的比是1:4,
第n个三角形的面积是
,
则第10个正△A10B10C10的面积是
,
故答案为:
.
| ||
| 4 |
| 3 |
| ||
| 40 |
∵△A2B2C2与△A1B1C1相似,并且相似比是1:2,
∴面积的比是1:4,
则正△A2B2C2的面积是
| 3 |
| 1 |
| 4 |
| ||
| 4 |
| ||
| 41 |
∵正△A3B3C3与正△A2B2C2的面积的比也是1:4,
∴面积是
| ||
| 4 |
| 1 |
| 4 |
| ||
| 16 |
| ||
| 42 |
依此类推△AnBnCn与△An-1Bn-1Cn-1的面积的比是1:4,
第n个三角形的面积是
| ||
| 4n-1 |
则第10个正△A10B10C10的面积是
| ||
| 49 |
故答案为:
| ||
| 49 |
点评:此题考查了相似三角形的判定与性质,以及等边三角形的性质,找出题中的规律是解题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
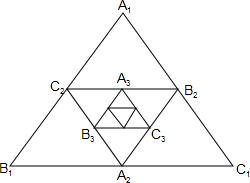 如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积.然后分别取△A1B1C1三边的中点A2、B2、C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积.用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第10个正△A10B10C10的面积是( )
如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积.然后分别取△A1B1C1三边的中点A2、B2、C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积.用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第10个正△A10B10C10的面积是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|






 B.
B. C.
C. D.
D.