题目内容
已知A、B两地相距6千米,小李从A地骑车去B地,小刘从B地步行去A地,若小李骑车的速度为12千米/小时,小刘步行的速度为3千米/小时,小刘先出发20分钟.
(1)求小刘走完全程需要多长时间?
(2)小李出发多长时间与小刘相遇?
(3)若小李到达B地休息30分钟后以另一速度返回A地,其他条件不变,小李从B地出发20分钟后又与小刘相遇,求小李从B地返回A地的速度.
(1)求小刘走完全程需要多长时间?
(2)小李出发多长时间与小刘相遇?
(3)若小李到达B地休息30分钟后以另一速度返回A地,其他条件不变,小李从B地出发20分钟后又与小刘相遇,求小李从B地返回A地的速度.
考点:一元一次方程的应用
专题:应用题
分析:(1)根据路程除以速度等于时间求出小刘走完全程需要的时间即可;
(2)设小李出发x小时与小刘相遇,根据A与B路程为6千米列出方程,求出方程的解即可得到结果;
(3)小李从B地返回A地的速度为y千米/小时,根据第二次相遇时小李比小刘多走了6千米的路程列出方程,求出方程的解即可得到结果.
(2)设小李出发x小时与小刘相遇,根据A与B路程为6千米列出方程,求出方程的解即可得到结果;
(3)小李从B地返回A地的速度为y千米/小时,根据第二次相遇时小李比小刘多走了6千米的路程列出方程,求出方程的解即可得到结果.
解答:解:(1)根据题意得:6÷3=2(小时),
则小刘走完全程需要2小时;
(2)设小李出发x小时与小刘相遇,
根据题意得:3(x+
)+12x=6,
解得:x=
,
由
小时=20分钟,
则小李出发20分钟与小刘相遇;
(3)设小李从B地返回A地的速度为y千米/小时,
根据题意得:
y-
×3=6,
解得:y=
.
则小李从B地返回A地的速度为
千米/小时.
则小刘走完全程需要2小时;
(2)设小李出发x小时与小刘相遇,
根据题意得:3(x+
| 20 |
| 60 |
解得:x=
| 1 |
| 3 |
由
| 1 |
| 3 |
则小李出发20分钟与小刘相遇;
(3)设小李从B地返回A地的速度为y千米/小时,
根据题意得:
| 30+20 |
| 60 |
| 20+30+20 |
| 60 |
解得:y=
| 57 |
| 5 |
则小李从B地返回A地的速度为
| 57 |
| 5 |
点评:此题考查了一元一次方程的应用,弄清相遇问题的实质是解本题的关键.

练习册系列答案
相关题目
一个正数的算术平方根是8,则这个数的相反数的立方根是( )
| A、4 | B、-4 | C、±4 | D、±8 |
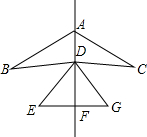 如图是一个风筝的图案,它是以直线为对称轴的轴对称图形,下列结论中不一定成立的是( )
如图是一个风筝的图案,它是以直线为对称轴的轴对称图形,下列结论中不一定成立的是( )| A、△ABD≌△ACD |
| B、AF垂直平分EG |
| C、直线BG,CE的交点在AF上 |
| D、△DEG是等边三角形 |
 如图,D是∠ABC内一点,BD=4,∠ABC=30°,设M是射线BA上一点,N是射线BC上一点,则△MND的周长的最小值是
如图,D是∠ABC内一点,BD=4,∠ABC=30°,设M是射线BA上一点,N是射线BC上一点,则△MND的周长的最小值是 如图,∠AOB=90°,∠AOC比∠BOC大28°,OD是∠AOB的平分线,求∠COD的度数.
如图,∠AOB=90°,∠AOC比∠BOC大28°,OD是∠AOB的平分线,求∠COD的度数.