Question

如图，梯形ABCD中，AD∥BC，∠C=90°，且AB=AD．连接BD，过点A作BD的垂线，交BC于点E，垂足为H．如果EC=3cm，CD=4cm，求梯形ABCD的面积．

Answer 1

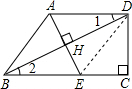解：连接DE，
∵∠C=90°，EC=3cm，CD=4cm，
∴DE=5．
∵AD∥BC，
∴∠1=∠2，
∵AB=AD，AH⊥BD，
∴BH=DH，∠AHD=∠EHB=90°
在△ADH和△EBH中，，
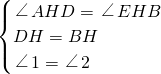∴△ADH≌△EBH（ASA），
∴BE=AD，
∴四边形ABED是平行四边形，
又∵AB=AD，
∴四边形ABED是菱形，
∴AD=BE=DE=5，
∴S_梯形ABCD=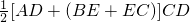==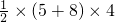26（cm²）．
分析：连接DE，因为AB=AD，AE⊥BD，AD∥BC，可证四边形ABED为菱形，从而得到AD=DE=BE==5，再根据梯形面积公式求出面积．
点评：本题考查了梯形、全等三角形和菱形的判定与性质，关键是根据条件能够发现图中的菱形ABDE．求得该梯形的上底、下底，再根据面积公式进行计算．