题目内容
已知代数式-5x2+ax+bx2+2x-5的取值与x无关,求a、b的值.
考点:多项式
专题:
分析:原式合并同类项后,根据多项式的值与x无关,得出关于a与b的方程,求出a与b的值.
解答:解:-5x2+ax+bx2+2x-5=(-5+b)x2+(a+2)x-5,
∵代数式-5x2+ax+bx2+2x-5的取值与x无关,
∴-5+b=0,解得b=5
a+2=0,解得a=-2.
故a的值是-2、b的值是5.
∵代数式-5x2+ax+bx2+2x-5的取值与x无关,
∴-5+b=0,解得b=5
a+2=0,解得a=-2.
故a的值是-2、b的值是5.
点评:此题考查了整式的加减,涉及的知识有:合并同类项法则,熟练掌握法则是解本题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
以下五家银行行标中,是轴对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
若点P关于x轴的对称点的坐标是(2,3),则点P关于原点的对称点的坐标是( )
| A、(-3,-2) |
| B、(2,-3) |
| C、(-2,-3) |
| D、(-2,3) |
下列说法正确的是( )
| A、有理数的绝对值为正数 |
| B、如果两数之和为0,则这两个数的绝对值相等 |
| C、只有正数或负数才有相反数 |
| D、任何数都有倒数 |
 某市为了美化环境,计划在如图所示的三角形空地上种植草皮,已知这种草皮每平方米售价为a元,则购买这种草皮至少需要
某市为了美化环境,计划在如图所示的三角形空地上种植草皮,已知这种草皮每平方米售价为a元,则购买这种草皮至少需要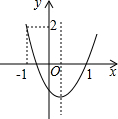 如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.给出四个结论:①abc<0;②b2-4ac>0;③a+b+c=0; ④a+c=1
如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.给出四个结论:①abc<0;②b2-4ac>0;③a+b+c=0; ④a+c=1 已知抛物线y=
已知抛物线y= 如图,AD为等边三角形的高,DE是△ADC的高,已知△ABC的边长为6,求AE的长.
如图,AD为等边三角形的高,DE是△ADC的高,已知△ABC的边长为6,求AE的长.