题目内容
如图,直线y=-
x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为______.

| 4 |
| 3 |

当x=0时,y=-
x+8=8,即B(0,8),
当y=0时,x=6,即A(6,0),
所以AB=AB′=10,即B′(-4,′0),
因为点B与B′关于AM对称,
所以BB′的中点为(
,
),即(-2,4)在直线AM上,
设直线AM的解析式为y=kx+b,把(-2,4);(6,0),
代入可得y=-
x+3,
故答案为y=-
x+3.
| 4 |
| 3 |
当y=0时,x=6,即A(6,0),
所以AB=AB′=10,即B′(-4,′0),
因为点B与B′关于AM对称,
所以BB′的中点为(
| 0-4 |
| 2 |
| 8+0 |
| 2 |
设直线AM的解析式为y=kx+b,把(-2,4);(6,0),
代入可得y=-
| 1 |
| 2 |
故答案为y=-
| 1 |
| 2 |

练习册系列答案
相关题目
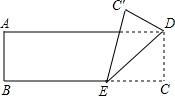



 与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.

