Question

（2014•宝山区一模）如图，梯形ABCD中，AD∥BC，BF⊥AD，CE⊥AD，且AF=EF=ED=5，BF=12，动点G从点A出发，沿折现AB-BC-CD以每秒1个单位长的速度运动到点D停止．设运动时间为t秒，△EFG的面积为y，则y关于t的函数图象大致是（　　）

A．

B．

C．

D．

Answer 1

分析：分三段考虑，①点G在AB上运动，②点G在BC上运动，③点G在CD上运动，分别求出y与t的函数表达式，继而可得出函数图象．

解答：解：在Rt△ABF中，AB=

AF2+BF 2

=13，在Rt△CED中，CD=

BF2+CF2

=13，
①点P在AB上运动：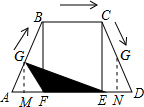
过点G作GM⊥AB于点M，则GM=AGsin∠A=

12

13

t，
此时y=

1

2

EF×GM=

30

13

t，为一次函数；
②点G在BC上运动，y=

1

2

BF×EF=30；
③点G在BC上运动，过点G作GN⊥AD于点N，则GN=DGsin∠D=

12

13

（AB+BC+CD-t）=

12(12-t)

13

，
则y=

1

2

EF×PN=

30(31-t)

13

，为一次函数．
综上可得选项A的图象符合．
故选A．

点评：本题考查了动点问题的函数图象，解答本题的关键是分段讨论y与t的函数关系式，当然在考试过程中，建议同学们直接判断是一次函数还是二次函数，不需要按部就班的解出解析式．