题目内容
如图,∠BAC=45º,AD⊥BC于点D,且BD=3,CD=2,则AD的长为???????? .
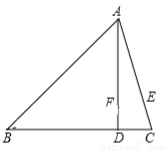
【答案】
6.
【解析】
试题分析:如 图,过B作BE⊥AC,垂足为E交AD于F,由∠BAC=45°可以得到BE=AE,再根据已知条件可以证明△AFE≌△BCE,可以得到 AF=BC=10,而∠FBD=∠DAC,又∠BDF=∠ADC=90°,由此可以证明△BDF∽△ADC,所以FD:DC=BD:AD,设FD长为x,则可建立关于x的方程,解方程即可求出FD,AD的长.
试题解析:如图,过B作BE⊥AC,垂足为E交AD于F

∵∠BAC=45°
∴BE=AE,
∵∠C+∠EBC=90°,∠C+∠EAF=90°,
∴∠EAF=∠EBC,
在△AFE与△BCE中,
 ,
,
∴△AFE≌△BCE(ASA)
∴AF=BC=BD+DC=10,∠FBD=∠DAC,
又∵∠BDF=∠ADC=90°
∴△BDF∽△ADC
∴FD:DC=BD:AD
设FD长为x
即x:2=3:(x+5)
解得x=1
即FD=1
∴AD=AF+FD=5+1=6.
考点: 1.相似三角形的判定与性质;2.解一元二次方程-公式法;3.全等三角形的判定与性质.

练习册系列答案
相关题目
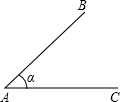 如图,∠BAC=45°,AB=4.现请你给定线段BC的长,使△ABC能构成等腰三角形.则BC的长可以是( )
如图,∠BAC=45°,AB=4.现请你给定线段BC的长,使△ABC能构成等腰三角形.则BC的长可以是( )| A、4 | ||
B、2
| ||
C、4或2
| ||
D、4或
|
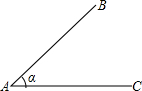 如图,∠BAC=45°,AB=6.现请你给定线段BC的长,使构成△ABC能构成等腰三角形.则BC的长可以是
如图,∠BAC=45°,AB=6.现请你给定线段BC的长,使构成△ABC能构成等腰三角形.则BC的长可以是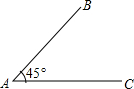 如图,∠BAC=45°,AB=6,要使△ABC惟一确定,那么BC的长度x满足的条件是
如图,∠BAC=45°,AB=6,要使△ABC惟一确定,那么BC的长度x满足的条件是 如图,∠BAC=45°,AB=6,点C在射线AP上.现请你给定线段AC的长,使△ABC能构成等腰三角形.则AC的长可以是
如图,∠BAC=45°,AB=6,点C在射线AP上.现请你给定线段AC的长,使△ABC能构成等腰三角形.则AC的长可以是