��Ŀ����
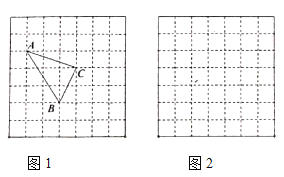
����Ŀ����ͼ��1������![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ��������һ�㣬
��������һ�㣬![]() Ϊ
Ϊ![]() ��һ���㣬�ֱ���
��һ���㣬�ֱ���![]() Ϊ�����ȱ�������
Ϊ�����ȱ�������![]() �͵ȱ�������
�͵ȱ�������![]() ������
������![]() .
.

��1����̽��![]() ��
��![]() ��λ�ù�ϵ����֤����
��λ�ù�ϵ����֤����
��2����ͼ��2����![]() Ϊ
Ϊ![]() �ӳ���������һ��ʱ����1���еĽ����Ƿ��������˵�����ɣ�
�ӳ���������һ��ʱ����1���еĽ����Ƿ��������˵�����ɣ�
��3����ͼ��3����![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬
�ӳ�����һ�㣬![]() Ϊ
Ϊ![]() ��һ���㣬�ֱ���
��һ���㣬�ֱ���![]() Ϊ��������������
Ϊ��������������![]() �͵���������
�͵���������![]() ��ʹ��
��ʹ��![]() ������
������![]() .Ҫʹ��1���еĽ�����Ȼ����������Ҫ����������������Ϊʲô��
.Ҫʹ��1���еĽ�����Ȼ����������Ҫ����������������Ϊʲô��
���𰸡���1��![]() ������������2��������
������������2��������![]() ������������3��Ҫʹ��1���еĽ�����Ȼ����������Ҫ���ӵ�������
������������3��Ҫʹ��1���еĽ�����Ȼ����������Ҫ���ӵ�������![]() ��������.
��������.
��������
��1��ͨ���ȱ������ε����ʣ���������ȡ���������ȣ����PF=PC��PE=PQ����EPF=��QPC��Ȼ�����ȫ�������ε��ж�����SAS֤����PFE�ա�PCQ���ٸ���ȫ�������ε����ʣ���Ӧ����ȣ�֪��EPF=��QPC=90������������ƽ���ߵ��ж�������ͬλ����ȣ���ֱ��ƽ�У�֪PF��AB�������ƽ���ߵ����ʣ���ƽ�����У���һ����ֱ�ڵ�����ֱ�ߣ�����һ��Ҳ��ֱ�ڵ�����ֱ�ߣ�֪EF��AB��
��2��ͨ���ȱ������ε����ʣ���������ȡ���������ȣ����PF=PC��PE=PQ����EPF=��QPC��Ȼ�����ȫ�������ε��ж�����SAS֤����PFE�ա�PCQ���ٸ���ȫ�������ε����ʣ���Ӧ����ȣ�֪��EPF=��QPC=90������������ƽ���ߵ��ж��������ڴ�����ȣ���ֱ��ƽ�У�֪PF��AB�������ƽ���ߵ����ʣ���ƽ�����У���һ����ֱ�ڵ�����ֱ�ߣ�����һ��Ҳ��ֱ�ڵ�����ֱ�ߣ�֪EF��AB��
��3����Ҫ���ӵ����������㣺![]() ���ڴ�����ȣ���ֱ��ƽ�У���
���ڴ�����ȣ���ֱ��ƽ�У���
��1��![]() ��֤�����£�
��֤�����£�
��![]() ��
��![]() ���ǵȱ������Σ�
���ǵȱ������Σ�
��![]() ��
��
��![]() ��
��
��![]()
��![]() ��
��![]() ��
��

��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]()
��2��������![]() ���������£�
���������£�
��![]() ��
��![]() ���ǵȱ������Σ�
���ǵȱ������Σ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��

��![]()
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() .
.
��3��Ҫʹ��1���еĽ�����Ȼ����������Ҫ���ӵ�������![]() ���������£�
���������£�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
����![]() ��
��
��![]() ��
��
��![]() .
.