题目内容
如图,四边形ABCD位于平面直角坐标系的第一象限,B、C在x轴上A点函数 上,且AB∥CD∥y轴,AD∥x轴,B(1,0)、C(3,0)。
上,且AB∥CD∥y轴,AD∥x轴,B(1,0)、C(3,0)。

⑴试判断四边形ABCD的形状。
⑵如图若点P是线段BD上一点PE⊥BC于E,M是PD的中点,连EM、AM。
求证:AM=EM

⑶在图中,连结AE交BD于N,则下列两个结论:

① 值不变;②
值不变;② 的值不变。其中有且仅有一个是正确的,请选择正确的结论证明并求其值。
的值不变。其中有且仅有一个是正确的,请选择正确的结论证明并求其值。
练习册系列答案
相关题目
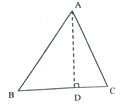
如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积..
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
过点A作AD⊥BC于点D,设BD=x,用含x的代数式表示CD | 根据勾股定理,利用AD作为“桥梁”,建立方程模型,求出x | 利用勾股定理求出AD的长,再计算三角形面积 |





 B.
B.  C.
C.  D.
D. 
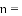
 变形,正确的是
变形,正确的是
 B.
B.  C.
C.  D.
D. 
 ,则x的取值范围是________
,则x的取值范围是________

 B.
B.  C.
C.  D.
D. 