题目内容
 如图∠PAC=30°在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F,再以O为坐标原点,AC所在直线为x轴,建立如图所示的坐标系.
如图∠PAC=30°在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F,再以O为坐标原点,AC所在直线为x轴,建立如图所示的坐标系.(1)求圆心O到射线AP的距离;
(2)将射线AP向左平移多少个单位与⊙O相切?并求切点的坐标.
分析:(1)作OG⊥AP于点G,在直角△AOG中利用直角三角形的性质求得OG即可;
(2)当A移动到A′时与圆相切,切点是M.连接OM,作MN⊥x轴于点N,再利用三角函数求得OA′的长,则平移的距离即可求解;在直角△A′MN中求得A′N,和MN,解求得ON的长,则M的坐标可以求得.
(2)当A移动到A′时与圆相切,切点是M.连接OM,作MN⊥x轴于点N,再利用三角函数求得OA′的长,则平移的距离即可求解;在直角△A′MN中求得A′N,和MN,解求得ON的长,则M的坐标可以求得.
解答: 解:(1)作OG⊥AP于点G.
解:(1)作OG⊥AP于点G.
∵在直角△AOG中,∠PAC=30°,OA=AD+OD=AD+
BD=8,
∴OG=
OA=4cm,
即圆心O到射线AP的距离是4cm;
(2)当A移动到A′时与圆相切,切点是M.连接OM,作MN⊥x轴于点N.
则∠AMO=90°,OM=5cm,
∵在直角△A′OM中,∠MA′O=30°
∴OA′=2OM=10cm,A′M=OA′•cos30°=5
cm.
∴AA′=OA′-OA=10-8=2cm.即将射线AP向左平移2个单位长度.
在直角△A′MN中,MN=A′M•sin30°=
(cm),
A′N=A′M•cos30°=5
×
=
(cm),
∴ON=OA′-A′N=10-
=2.5(cm).
故M的坐标是(2.5,
).
 解:(1)作OG⊥AP于点G.
解:(1)作OG⊥AP于点G.∵在直角△AOG中,∠PAC=30°,OA=AD+OD=AD+
| 1 |
| 2 |
∴OG=
| 1 |
| 2 |
即圆心O到射线AP的距离是4cm;
(2)当A移动到A′时与圆相切,切点是M.连接OM,作MN⊥x轴于点N.
则∠AMO=90°,OM=5cm,
∵在直角△A′OM中,∠MA′O=30°
∴OA′=2OM=10cm,A′M=OA′•cos30°=5
| 3 |
∴AA′=OA′-OA=10-8=2cm.即将射线AP向左平移2个单位长度.
在直角△A′MN中,MN=A′M•sin30°=
5
| ||
| 2 |
A′N=A′M•cos30°=5
| 3 |
| ||
| 2 |
| 15 |
| 2 |
∴ON=OA′-A′N=10-
| 15 |
| 2 |
故M的坐标是(2.5,
5
| ||
| 2 |
点评:本题考查了三角函数以及切线的性质,正确求得A′N的长度是关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
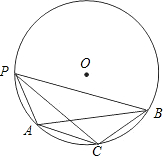 如图,点P是圆上的一个动点,弦AB=
如图,点P是圆上的一个动点,弦AB= 下列说法:
下列说法: 如图,P是等边三角形ABC内的一点,若将△PAC绕点A逆时针旋转到△P′AB,则∠PAP′的度数为( )
如图,P是等边三角形ABC内的一点,若将△PAC绕点A逆时针旋转到△P′AB,则∠PAP′的度数为( )