题目内容
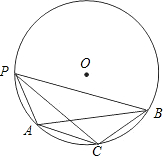 如图,点P是圆上的一个动点,弦AB=
如图,点P是圆上的一个动点,弦AB=| 3 |
(1)当∠PAC等于多少度时,四边形PACB有最大面积,最大面积是多少?
(2)当∠PAC等于多少度时,四边形PACB是梯形,说明你的理由.
分析:(1)由PC是∠APB的平分线,可知
=
,根据直径所对的圆周角是直角,根据特殊角的三角函数值求出PC的值,即可求出四边形PACB的面积.
(2)当∠PAC=120°时,根据PC是∠APB的平分线,求出∠PAC与∠APB互补,即AC∥PB且AP与BC不平行,四边形PACB是梯形;
当∠PAC=60°时,由
=
可知,AC=BC,又因为∠BAC=30°,所以∠ACB=120°,∠PAC与∠ACB互补,故BC∥AP且AC与PB不平行,四边形PACB是梯形.
 |
| AC |
 |
| BC |
(2)当∠PAC=120°时,根据PC是∠APB的平分线,求出∠PAC与∠APB互补,即AC∥PB且AP与BC不平行,四边形PACB是梯形;
当∠PAC=60°时,由
 |
| AC |
 |
| BC |
解答:解:(1)∵PC是∠APB的平分线,
∴
=
.(1分)
当PC是圆的直径,即∠PAC=90°时,四边形PACB面积最大.(3分)
在Rt△PAC中,∠APC=30°,AP=PB=AB=
,
∴PC=
=
•
=2.(4分)
∴S四边形PACB=2S△ACP(5分)
=
PC•AB=
×2×
=
.(6分)
(2)当∠PAC=120°时,四边形PACB是梯形.(7分)
∵PC是∠APB的平分线,
∴∠APC=∠BPC=∠CAB=30°.
∴∠APB=60°.
∴∠PAC+∠APB=180°.
∴AC∥PB且AP与BC不平行.
∴四边形PACB是梯形.(8分)
当∠PAC=60°时,四边形PACB是梯形.(9分)
∵
=
,
∴AC=BC.
又∵∠BAC=30°,
∴∠ACB=120°.
∴∠PAC+∠ACB=180°.
∴BC∥AP且AC与PB不平行.
∴四边形PACB是梯形.(10分)
∴
 |
| AC |
 |
| BC |
当PC是圆的直径,即∠PAC=90°时,四边形PACB面积最大.(3分)
在Rt△PAC中,∠APC=30°,AP=PB=AB=
| 3 |
∴PC=
| AP |
| cos30° |
| 3 |
| 2 | ||
|
∴S四边形PACB=2S△ACP(5分)
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
=
| 3 |
(2)当∠PAC=120°时,四边形PACB是梯形.(7分)
∵PC是∠APB的平分线,
∴∠APC=∠BPC=∠CAB=30°.
∴∠APB=60°.
∴∠PAC+∠APB=180°.
∴AC∥PB且AP与BC不平行.
∴四边形PACB是梯形.(8分)
当∠PAC=60°时,四边形PACB是梯形.(9分)
∵
 |
| AC |
 |
| BC |
∴AC=BC.
又∵∠BAC=30°,
∴∠ACB=120°.
∴∠PAC+∠ACB=180°.
∴BC∥AP且AC与PB不平行.
∴四边形PACB是梯形.(10分)
点评:本题属动态性题目,考查的是角平分线的性质,梯形,圆心角、弧、弦的关系及解直角三角形的关系,是一道综合性较好的题目的题目.

练习册系列答案
相关题目
 若S△ABC=25,AB=10,点O移动到何处⊙O与AC相切于点F?
若S△ABC=25,AB=10,点O移动到何处⊙O与AC相切于点F?
 是圆O的一条弦,
是圆O的一条弦, ,垂足为
,垂足为 ,交圆O于点
,交圆O于点 ,点
,点 在圆O上.(1)若
在圆O上.(1)若 ,求
,求 的度数;
的度数;
 ,
, ,求
,求 是圆O的一条弦,
是圆O的一条弦, ,垂足为
,垂足为 ,交圆O于点
,交圆O于点 ,点
,点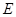 在圆O上.(1)若
在圆O上.(1)若 ,求
,求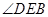 的度数;
的度数; ,
, ,求
,求
 的图象上的点,点B,C的坐标分别为B(-
的图象上的点,点B,C的坐标分别为B(- ,-
,- ),C(
),C( ,
, ).试利用性质:“函数y=
).试利用性质:“函数y= 的图象上任意一点A都满足|AB-AC|=2
的图象上任意一点A都满足|AB-AC|=2 ”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y=
”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y= 的图象上运动时,点F总在一条曲线上运动,则这条曲线为( )
的图象上运动时,点F总在一条曲线上运动,则这条曲线为( )