题目内容
如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )

|
| A. |
| B. |
| C. |
| D. |
|
D解:连接AC1,
∵四边形AB1C1D1是正方形,
∴∠C1AB1= ×90°=45°=∠AC1B1,
×90°=45°=∠AC1B1,
∵边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,
∴∠B1AB=45°,
∴∠DAB1=90°﹣45°=45°,
∴AC1过D点,即A、D、C1三点共线,
∵正方形ABCD的边长是1,
∴四边形AB1C1D1的边长是1,
在Rt△C1 D1A中,由勾股定理得:AC1=
D1A中,由勾股定理得:AC1= =
= ,
,
则DC1= ﹣1,
﹣1,
∵∠AC1B1=45°,∠C1DO=90°,
∴∠C1OD=45°=∠DC1O,
∴DC1=OD= ﹣1,
﹣1,
∴S△ADO= ×OD•AD=
×OD•AD= ,
,
∴四边形AB1OD的面积是=2× =
= ﹣1,
﹣1,
故选:D.


练习册系列答案
相关题目
一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则购买盒子所需要最少费用为 元.
| 型号 | A | B |
| 单个盒子容量(升) | 2 | 3 |
| 单价(元) | 5 | 6 |



 ﹣1
﹣1 恰有两个整数解,则m的取值范围是( )
恰有两个整数解,则m的取值范围是( )




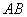 于点
于点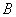 ,点
,点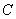 在
在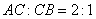 ,点
,点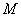 是直线上的动点,作点
是直线上的动点,作点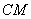 的对称点
的对称点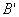 ,直线
,直线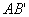 与直线
与直线 ,连接
,连接
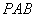 = °,线段
= °,线段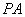 与
与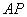 相交于
相交于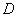 ,
, 。
。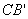 ;②
;②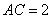 ,
, ,则满足条件
,则满足条件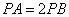 的点都在一个确定的圆上,在
的点都在一个确定的圆上,在