题目内容
直线y= x-2与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
x-2与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).(1)求抛物线的解析式;
(2)在直线AC上方的抛物线上有一动点D,当D与直线AC的距离DE最大时,求出点D的坐标,并求出最大距离是多少?

【答案】分析:(1)首先求出点A,点C的坐标;然后利用待定系数法求出抛物线的解析式;
(2)AC为定值,当DE最大时,△ACD的面积最大,因此只需要求出△ACD面积的最大值即可.如解答图所示,作辅助线,利用S△ACD=S梯形AGFC-S△CDF-S△ADG求出S△ACD的表达式,然后利用二次函数的性质求出最大值,并进而求出点D的坐标和DE的最大值.
解答:解:(1)在直线解析式y= x-2中,令x=0,得y=-2;令y=0,得x=4,
x-2中,令x=0,得y=-2;令y=0,得x=4,
∴A(4,0),C(0,-2).
设抛物线的解析式为y=ax2+bx+c,
∵点A(4,0),B(1,0),C(0,-2)在抛物线上,
∴ ,
,
解得a= ,b=
,b= ,c=-2.
,c=-2.
∴抛物线的解析式为:y= x2+
x2+ x-2.
x-2.
(2)设点D坐标为(x,y),则y= x2+
x2+ x-2.
x-2.
在Rt△AOC中,OA=4,OC=2,由勾股定理得:AC= .
.
如答图1所示,连接CD、AD.
过点D作DF⊥y轴于点F,过点A作AG⊥FD交FD的延长线于点G,
则FD=x,DG=4-x,OF=AG=y,FC=y+2.

S△ACD=S梯形AGFC-S△CDF-S△ADG= (AG+FC)•FG-
(AG+FC)•FG- FC•FD-
FC•FD- DG•AG=
DG•AG= (y+y+2)×4-
(y+y+2)×4- (y+2)•x-
(y+2)•x- (4-x)•y
(4-x)•y
=2y-x-4
将y= x2+
x2+ x-2代入得:S△ACD=2y-x-4=-x2+4x=-(x-2)2+4,
x-2代入得:S△ACD=2y-x-4=-x2+4x=-(x-2)2+4,
∴当x=2时,△ACD的面积最大,最大值为4.
当x=2时,y=1,∴D(2,1).
∵S△ACD= AC•DE,AC=
AC•DE,AC= ,
,
∴当△ACD的面积最大时,高DE最大,
则DE的最大值为: =
= =
= .
.
∴当D与直线AC的距离DE最大时,点D的坐标为(2,1),最大距离为 .
.
点评:本题是二次函数的综合题,考查了二次函数的图象与性质、待定系数法、最值、图形面积计算等知识点,难度不大.第(2)问有多种解法,同学们可以从不同角度尝试与探究.
(2)AC为定值,当DE最大时,△ACD的面积最大,因此只需要求出△ACD面积的最大值即可.如解答图所示,作辅助线,利用S△ACD=S梯形AGFC-S△CDF-S△ADG求出S△ACD的表达式,然后利用二次函数的性质求出最大值,并进而求出点D的坐标和DE的最大值.
解答:解:(1)在直线解析式y=
 x-2中,令x=0,得y=-2;令y=0,得x=4,
x-2中,令x=0,得y=-2;令y=0,得x=4,∴A(4,0),C(0,-2).
设抛物线的解析式为y=ax2+bx+c,
∵点A(4,0),B(1,0),C(0,-2)在抛物线上,
∴
 ,
,解得a=
 ,b=
,b= ,c=-2.
,c=-2.∴抛物线的解析式为:y=
 x2+
x2+ x-2.
x-2.(2)设点D坐标为(x,y),则y=
 x2+
x2+ x-2.
x-2.在Rt△AOC中,OA=4,OC=2,由勾股定理得:AC=
 .
.如答图1所示,连接CD、AD.
过点D作DF⊥y轴于点F,过点A作AG⊥FD交FD的延长线于点G,
则FD=x,DG=4-x,OF=AG=y,FC=y+2.

S△ACD=S梯形AGFC-S△CDF-S△ADG=
 (AG+FC)•FG-
(AG+FC)•FG- FC•FD-
FC•FD- DG•AG=
DG•AG= (y+y+2)×4-
(y+y+2)×4- (y+2)•x-
(y+2)•x- (4-x)•y
(4-x)•y=2y-x-4
将y=
 x2+
x2+ x-2代入得:S△ACD=2y-x-4=-x2+4x=-(x-2)2+4,
x-2代入得:S△ACD=2y-x-4=-x2+4x=-(x-2)2+4,∴当x=2时,△ACD的面积最大,最大值为4.
当x=2时,y=1,∴D(2,1).
∵S△ACD=
 AC•DE,AC=
AC•DE,AC= ,
,∴当△ACD的面积最大时,高DE最大,
则DE的最大值为:
 =
= =
= .
.∴当D与直线AC的距离DE最大时,点D的坐标为(2,1),最大距离为
 .
.点评:本题是二次函数的综合题,考查了二次函数的图象与性质、待定系数法、最值、图形面积计算等知识点,难度不大.第(2)问有多种解法,同学们可以从不同角度尝试与探究.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 内作Rt△ABC,∠BAC=90°.
内作Rt△ABC,∠BAC=90°.
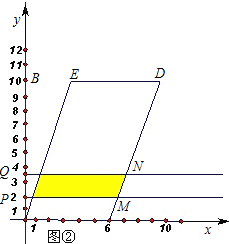
 过B、C分别作y轴的平行线交双曲线
过B、C分别作y轴的平行线交双曲线 (2012•鄂州)直线y=-
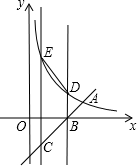
(2012•鄂州)直线y=- (2013•威海)如图,在平面直角坐标系中,直线y=
(2013•威海)如图,在平面直角坐标系中,直线y=