题目内容
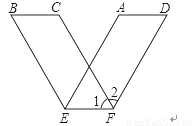
用平行四边形纸条沿对边AB、CD上的点E、F所在的直线折成V字形图案，已知图中∠1=62°，则∠2的度数是________
56°
【解析】试题分析：根据题意得：2∠1+∠2=180°，
∴∠2=180°-2×62°=56°．
练习册系列答案
相关题目
某厂原计划在规定时间内生产通讯设备60台，由于改进了操作技术，每天生产的 台数比原计划多50％，结果提前两天完成任务．求改进操作技术后每天生产通讯设备多少台．
15台．
【解析】试题分析：设改进操作技术前每天生产通讯设备x台，则改进操作技术后每天生产通讯设备1.5x台，根据提前两天完成任务，列方程求解即可．
试题解析：设改进技术前每天生产x台，根据题意，得，解得x＝10，
经检验x＝10是原方程的解，
则1.5x＝15，
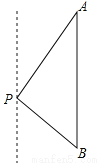
所以改进操作技术后每天生产通讯设备15台． 如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为（ ）
A. 40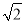
海里 B. 40
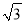海里 C. 80海里 D. 40
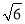海里
A
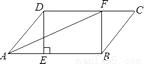
【解析】试题分析：过点P作PD⊥AB于点D，根据方位角可得：∠A=30°，∠B=45°，根据AP=80海里可得PD=40海里，PB=40海里，故选A． 在平行四边形ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．
（1）求证：四边形BFDE是矩形；
（2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB．
（1）证明见解析（2）证明见解析
【解析】试题分析：（1）根据平行四边形的性质，可得AB与CD的关系，根据平行四边形的判定，可得BFDE是平行四边形，再根据矩形的判定，可得答案；
（2）根据平行线的性质，可得∠DFA=∠FAB，根据等腰三角形的判定与性质，可得∠DAF=∠DFA，根据角平分线的判定，可得答案．
试题分析：（1）证明：∵四边形ABCD是平行四边形，
∴AB∥C... 如图，在□ABCD中，点M为CD的中点，且DC=2AD，则AM与BM的夹角的度数为（ ）
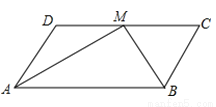
A. 100° B. 95° C. 90° D. 85°
C
【解析】试题解析： 中，
∴DC∥AB，AD∥BC，
∴∠DAB+∠CBA=180°，∠BAM=∠DMA，
∵点M为CD的中点，且DC=2AD，
∴DM=AD，
∴∠DMA=∠DAM，
∴∠DAM=∠BAM，
同理∠ABM=∠CBM，
即：
∴∠AMB=180°-90°=90°．
故选C． 平行四边形ABCD的周长32，5AB=3BC，则对角线AC的取值范围为（ ）
A．6＜AC＜10 B.6＜AC＜16 C.10＜AC＜16 D.4＜AC＜16
D．
【解析】
试题分析：∵平行四边形ABCD的周长32，5AB=3BC，∴2（AB+BC）=2（BC+BC）=32，
∴BC=10，∴AB=6，∴BC﹣AB＜AC＜BC+AB，即4＜AC＜16．
故选D． n边形的边数增加一倍,它的内角和增加( )
A. 180° B. 360° C. (n-2)·180° D. n180°
D
【解析】∵n边形的内角和是（n-2）•180°，
∴2n边形的内角和是（2n-2）•180°，
∴将n边形的边数增加一倍，则它的内角和增加：（2n-2）•180°-（n-2）•180°=n180°，
故选D. 有三个连续正整数,其倒数之和是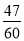
,那么这三个数中最小的是（ ）
A. 1 B. 2 C. 3 D. 4
C
【解析】设三个连续正整数分别为： ，根据题意得：
解得： 则 .
故选C.