题目内容
甲乙两船从位于南北走向的海岸线上的港口A同时出发，甲以每小时30海里的速度向北偏东35°方向航行，乙船以每小时40海里的速度向另一方向航行，2小时后，甲船到C岛，乙船到达B岛，B、C两岛相距100海里，判断乙船所走方向，说明理由．
考点：勾股定理的逆定理
专题：应用题
分析：首先计算出甲乙两船的路程，再根据勾股定理逆定理可证明∠BAC=90°，然后再根据C岛在A北偏东35°方向，可得B岛在A北偏西55°方向．
解答：
解：由题意得：甲2小时的路程=30×2=60海里，乙2小时的路程=40×2=80海里，
∵602+802=1002，
∴∠BAC=90°，
∵C岛在A北偏东35°方向，
∴B岛在A北偏西55°方向．
∴乙船所走方向是北偏西55°方向．
解：由题意得：甲2小时的路程=30×2=60海里，乙2小时的路程=40×2=80海里，∵602+802=1002，
∴∠BAC=90°，
∵C岛在A北偏东35°方向，
∴B岛在A北偏西55°方向．
∴乙船所走方向是北偏西55°方向．
点评：此题主要考查了勾股定理逆定理，关键是掌握勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．
练习册系列答案
阅读快车系列答案
相关题目
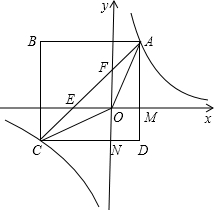如图，矩形ABCD（点A在第一象限）与x轴的正半轴相交于M，与y的负半轴相交于N，AB∥x轴，反比例函数的图象y=
如图，在矩形ABCD中，对角线AC、BD交于点O，若∠AOD=120°，AB=2，则AD=