题目内容
14.解下列方程:(1)x2+8x+6=0;
(2)(x-2)2=(2x+3)2.
分析 (1)先把常数项移到等式右边,然后等式两边同时加上一次项系数一半的平方,再根据完全平方公式因式分解即可.
(2)先移项,然后利用平方差公式进行因式分解.
解答 解:(1)x2+8x+6=0,
x2+8x=-6,
x2+8x+16=-6+16,
(x+4)2=10,
x+4=±$\sqrt{10}$,
则x1=-4+$\sqrt{10}$,x2=-4-$\sqrt{10}$;
(2)(x-2)2=(2x+3)2,
(x-2)2-(2x+3)2=0,
(x-2+2x+3)(x-2-2x-3)=0,
-(3x+1)(x+5)=0,
则x1=-$\frac{1}{3}$,x2=5.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
5.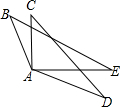 如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是( )
如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是( )
 如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是( )
如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是( )| A. | ∠B=∠C | B. | ∠D=∠E | C. | ∠BAC=∠EAD | D. | ∠B=∠E |
19.两圆的圆心都是O,半径分别为r1,r2(r1<r2),若r1<OP<r2,则点P在( )
| A. | 大圆外 | B. | 小圆内 | C. | 大圆内,小圆外 | D. | 无法确定 |
4.某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件,第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低2元,可多售出60件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余T恤清仓销售,清仓时单价为40元,设第二个月单价降低x元.
(1)填表(不需要化简)
(2)若批发商希望通过销售这批T恤获利15000元,则第二个月的单价应是多少元?
(1)填表(不需要化简)
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价/元 | 80 | 80-x | 40 |
| 销售量/件 | 200 | 200+30x | 800-200-(200+30x) |
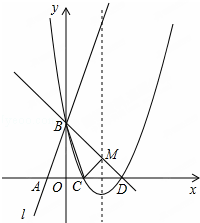 如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).