题目内容
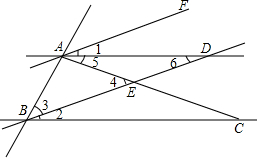 已知:如图,直线AF∥BD,且∠1=∠2=20°.
已知:如图,直线AF∥BD,且∠1=∠2=20°.(1)求证:AD∥BC;(证明过程必须批注依据)
(2)若∠3=∠4,∠5=∠6,求∠ABC的度数.
考点:平行线的判定与性质
专题:
分析:(1)欲证明AD∥BC,只需证得∠GAD=∠ABC即可;
(2)利用(1)中的平行线的性质求得∠5=∠6=∠1=20°,由三角形外角的性质可以求得∠3=∠4=2∠5=40°,结合图形来求∠ABC的度数.
(2)利用(1)中的平行线的性质求得∠5=∠6=∠1=20°,由三角形外角的性质可以求得∠3=∠4=2∠5=40°,结合图形来求∠ABC的度数.
解答: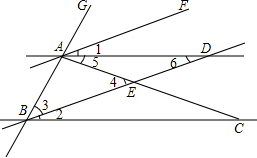 (1)证明:如图,∵AF∥BD(已知),
(1)证明:如图,∵AF∥BD(已知),
∴∠CAF=∠3(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠GAF+∠1=∠3+∠2,即∠GAD=∠ABC(等量代换),
∴AD∥BC(同位角相等,两直线平行);
(2)解:∵由(1)知,AD∥BC,
∴∠1=∠6=20°.
又∵∠5=∠6,∠4=∠5+∠6,
∴∠5=20°,∠4=40°.
∵∠3=∠4,
∴∠3=40°,
∴∠ABC=∠2+∠3=60°.
 (1)证明:如图,∵AF∥BD(已知),
(1)证明:如图,∵AF∥BD(已知),∴∠CAF=∠3(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠GAF+∠1=∠3+∠2,即∠GAD=∠ABC(等量代换),
∴AD∥BC(同位角相等,两直线平行);
(2)解:∵由(1)知,AD∥BC,
∴∠1=∠6=20°.
又∵∠5=∠6,∠4=∠5+∠6,
∴∠5=20°,∠4=40°.
∵∠3=∠4,
∴∠3=40°,
∴∠ABC=∠2+∠3=60°.
点评:本题考查了平行线的判定与性质.平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
相关题目
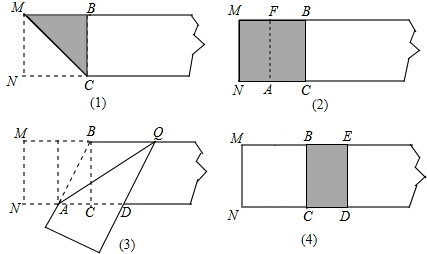
 阅读下列材料,并解答以下问题.
阅读下列材料,并解答以下问题.