题目内容
如图1,Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.
(1)求证:CE=CF;
(2)将图1中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其他条件不变,如图2,求证:A′E′是∠CE′D′的角平分线;
(3)试猜想:BE′与CF有怎样的数量关系?请证明你的结论.
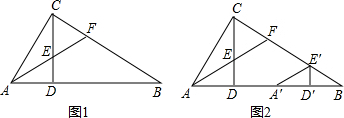
(1)求证:CE=CF;
(2)将图1中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其他条件不变,如图2,求证:A′E′是∠CE′D′的角平分线;
(3)试猜想:BE′与CF有怎样的数量关系?请证明你的结论.

考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:(1)根据角平分线的定义可得∠1=∠2,再根据等角的余角相等求出∠CFE=∠AED,然后根据对顶角相等可得∠CEF=∠AED,从而得到∠CEF=∠CFE,再根据等角对等边证明即可;
(2)根据平移的性质可得∠A′E′D′=∠AED,A′E′∥AE,再根据两直线平行,同位角相等可得∠CFE=∠A′E′F,然后求出∠A′E′D′=∠A′E′F,根据角平分线的定义证明即可;
(3)根据平移的性质可得∠2=∠3,AE=A′E′,求出∠1=∠3,再根据等角的余角相等求出∠B=∠4,再利用“角角边”证明△ACE和△A′BE′全等,根据全等三角形对应边相等可得BE′=CE,从而得到BE′=CF.
(2)根据平移的性质可得∠A′E′D′=∠AED,A′E′∥AE,再根据两直线平行,同位角相等可得∠CFE=∠A′E′F,然后求出∠A′E′D′=∠A′E′F,根据角平分线的定义证明即可;
(3)根据平移的性质可得∠2=∠3,AE=A′E′,求出∠1=∠3,再根据等角的余角相等求出∠B=∠4,再利用“角角边”证明△ACE和△A′BE′全等,根据全等三角形对应边相等可得BE′=CE,从而得到BE′=CF.
解答:证明:(1)∵AF平分∠CAB,
∴∠1=∠2,
∵∠ACB=90°,CD⊥AB,
∴∠1+∠CFE=90°,∠2+∠AED=90°,
∴∠CFE=∠AED,
∵∠CEF=∠AED(对顶角相等),
∴∠CEF=∠CFE,
∴CE=CF;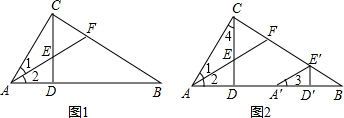
(2)∵△ADE沿AB向右平移得到△A′D′E′,
∴∠A′E′D′=∠AED,A′E′∥AE,
∴∠CFE=∠A′E′F,
∵∠CFE=∠AED,
∴∠A′E′D′=∠A′E′F,
∴A′E′是∠CE′D′的角平分线;
(3)由平移的性质得,∠2=∠3,AE=A′E′,
∴∠1=∠3,
∵∠ACB=90°,CD⊥AB,
∴∠4+∠BAC=90°,∠B+∠BAC=90°,
∴∠B=∠4,
在△ACE和△A′BE′中,
,
∴△ACE≌△A′BE′(AAS),
∴BE′=CE,
∵CE=CF,
∴BE′=CF.
∴∠1=∠2,
∵∠ACB=90°,CD⊥AB,
∴∠1+∠CFE=90°,∠2+∠AED=90°,
∴∠CFE=∠AED,
∵∠CEF=∠AED(对顶角相等),
∴∠CEF=∠CFE,
∴CE=CF;

(2)∵△ADE沿AB向右平移得到△A′D′E′,
∴∠A′E′D′=∠AED,A′E′∥AE,
∴∠CFE=∠A′E′F,
∵∠CFE=∠AED,
∴∠A′E′D′=∠A′E′F,
∴A′E′是∠CE′D′的角平分线;
(3)由平移的性质得,∠2=∠3,AE=A′E′,
∴∠1=∠3,
∵∠ACB=90°,CD⊥AB,
∴∠4+∠BAC=90°,∠B+∠BAC=90°,
∴∠B=∠4,
在△ACE和△A′BE′中,
|
∴△ACE≌△A′BE′(AAS),
∴BE′=CE,
∵CE=CF,
∴BE′=CF.
点评:本题考查了全等三角形的判定与性质,角平分线的定义,平移的性质,等角的余角相等的性质,熟记各性质以及三角形全等的判定方法是解题的关键,利用数字加弧线表示角更形象直观.

练习册系列答案
相关题目
已知等腰三角形的一个角为72°,则其顶角为( )
| A、36° | B、45° |
| C、60° | D、72°或36° |