题目内容
点P是△ABC内任意一点,则∠BPC与∠A的大小关系是
- A.∠BPC<∠A
- B.∠BPC>∠A
- C.∠BPC=∠A
- D.无法确定
B
分析:根据三角形内角和外角的关系解答即可.
解答:连接BP并延长交AC于D,连接CP,

在△BDC中,∠BPC>∠BDC,
在△ABD中∠BDC>∠A,因而∠BPC>∠A.
∴∠BPC与∠A的大小关系是∠BPC>∠A.
故选B.
点评:解答此题的关键是作出辅助线,利用三角形外角的性质定理.
分析:根据三角形内角和外角的关系解答即可.
解答:连接BP并延长交AC于D,连接CP,

在△BDC中,∠BPC>∠BDC,
在△ABD中∠BDC>∠A,因而∠BPC>∠A.
∴∠BPC与∠A的大小关系是∠BPC>∠A.
故选B.
点评:解答此题的关键是作出辅助线,利用三角形外角的性质定理.

练习册系列答案
相关题目

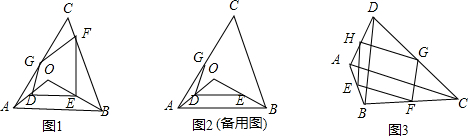
 如图,点O是△ABC内任意一点,G、D、E分别为AC、OA、OB的中点,F为BC上一动点,问四边形GDEF能否为平行四边形?若可以,指出F点位置,并给予证明.
如图,点O是△ABC内任意一点,G、D、E分别为AC、OA、OB的中点,F为BC上一动点,问四边形GDEF能否为平行四边形?若可以,指出F点位置,并给予证明.