题目内容
(1)如图1,点O是△ABC内任意一点,G、D、E分别为AC、OA、OB的中点,F为BC上一动点,问四边形GDEF能否为平行四边形?若可以,指出F点位置,并给予证明;(2)(填空,使下列命题成立,不要求证明)如图3,点E、F、G、H分别为AB、BC、CD、DA的中点.
当
当
当
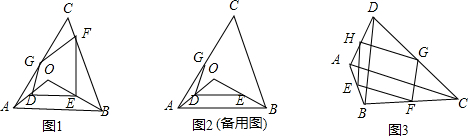
分析:当F为BC中点时,四边形GDEF为平行四边形,因为连接OC后将把四边形AOBC分成两个三角形,然后根据三角形中位线平行且等于第三边的一半,来证明GD、FE即平行且相等,从而得出为平行四边形.
解答:解:(1)答:当F为BC中点时,四边形GDEF为平行四边形(2分)
证明:∵G、F分别是AC、BC中点
∴GF∥AB,且GF=
AB(2分)
同理可得,DE∥AB,且DE=
AB(2分)
∴GF∥DE,且GF=DE
∴四边形GDEF是平行四边形(2分)
(2)DB⊥AC(1分);DB=AC(1分);DB⊥AC,且DB=AC(2分).
证明:∵G、F分别是AC、BC中点
∴GF∥AB,且GF=
| 1 |
| 2 |
同理可得,DE∥AB,且DE=
| 1 |
| 2 |
∴GF∥DE,且GF=DE
∴四边形GDEF是平行四边形(2分)
(2)DB⊥AC(1分);DB=AC(1分);DB⊥AC,且DB=AC(2分).
点评:此题主要考查了平行四边形的判定及性质,以及矩形、菱形、正方形的判定,比较全面,难易程度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
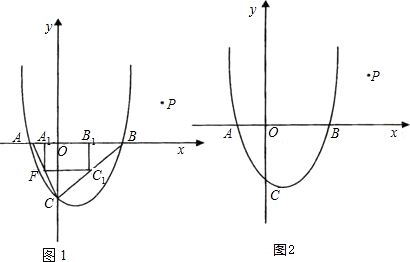

 如图,若点P是反比例函数y=
如图,若点P是反比例函数y=