题目内容
(1)x3-4x
(2)4a2-36ab+81b2
(3)(a2+ab+b2)2-9a2b2
(4)已知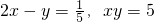 ,求4x3y-4x2y2+xy3的值.
,求4x3y-4x2y2+xy3的值.
(5’×4)
解:(1)原式=x(x2-4)
=x(x-2)(x+2);
(2)原式=(2a)2-2•2a•9b+(9b)2
=(2a-9b)2;
(3)原式=(a2+ab+b2)2-(3ab)2
=(a2+ab+b2+3ab)(a2+ab+b2-3ab)
=(a2+4ab+b2)(a2-2ab+b2)
=(a2+4ab+b2)(a-b)2;
(4)原式=xy(4x2-4xy+y2)
=xy(2x-y)2
当xy=5,2x-y= 时,原式=5×
时,原式=5×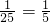 .
.
分析:(1)有公因式x,先提取x,再运用平方差公式进行分解即可;
(2)采用完全平方公式分解即可;
(3)先用平方差公式进行因式分解,进而能用完全平方公式分解的式子用完全平方公式继续分解;
(4)先提取公因式xy,再把相关值代入求解.
点评:分解因式的方法和规律:多项式有2项时考虑提公因式法和平方差公式;多项式有3项时考虑提公因式法和完全平方公式;注意分解因式的结果一定要分解到底.
解:(1)原式=x(x2-4)
=x(x-2)(x+2);
(2)原式=(2a)2-2•2a•9b+(9b)2
=(2a-9b)2;
(3)原式=(a2+ab+b2)2-(3ab)2
=(a2+ab+b2+3ab)(a2+ab+b2-3ab)
=(a2+4ab+b2)(a2-2ab+b2)
=(a2+4ab+b2)(a-b)2;
(4)原式=xy(4x2-4xy+y2)
=xy(2x-y)2
当xy=5,2x-y=
 时,原式=5×
时,原式=5×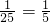 .
.分析:(1)有公因式x,先提取x,再运用平方差公式进行分解即可;
(2)采用完全平方公式分解即可;
(3)先用平方差公式进行因式分解,进而能用完全平方公式分解的式子用完全平方公式继续分解;
(4)先提取公因式xy,再把相关值代入求解.
点评:分解因式的方法和规律:多项式有2项时考虑提公因式法和平方差公式;多项式有3项时考虑提公因式法和完全平方公式;注意分解因式的结果一定要分解到底.

练习册系列答案
相关题目