题目内容
直角△ABC的三条边a、b、c均满足方程x2-(
+1)x+m=0,则①m= ;②△ABC的面积为 .
| 2 |
考点:根的判别式,等腰直角三角形
专题:
分析:因为一元二次方程有两个不相等的实数根,而直角△ABC的三边a、b、c均满足方程,则该直角三角形一定是等腰直角三角形.根据等腰直角三角形的斜边是直角边的
倍,可以求得方程的两个根,其中较小的根是等腰直角三角形的直角边,进一步求得三角形的面积即可.
| 2 |
解答:解:∵直角△ABC的三条边a、b、c均满足方程x2-(
+1)x+m=0的两个根,
必然存在a=b或a=c或b=c
∴直角三角形△ABC是等腰直角三角形,则斜边是直角边的
倍.
设方程的较小的根是x,则较大的根是
x.根据根与系数的关系,得
x+
x=
+1
解得x=1,
x•
x=m,
m=
则直角三角形的直角边是1,直角三角形的面积是
.
| 2 |
必然存在a=b或a=c或b=c
∴直角三角形△ABC是等腰直角三角形,则斜边是直角边的
| 2 |
设方程的较小的根是x,则较大的根是
| 2 |
x+
| 2 |
| 2 |
解得x=1,
x•
| 2 |
m=
| 2 |
则直角三角形的直角边是1,直角三角形的面积是
| 1 |
| 2 |
点评:此题考查了一元二次方程根与系数的关系,抓住等腰直角三角形的性质解决问题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,已知⊙O1的半径为1cm,⊙O2的半径为4cm,将⊙O1,⊙O2放置在直线l上,如果⊙O1在直线l上任意滚动,那么圆心距O1O2的长不可能是( )
如图,已知⊙O1的半径为1cm,⊙O2的半径为4cm,将⊙O1,⊙O2放置在直线l上,如果⊙O1在直线l上任意滚动,那么圆心距O1O2的长不可能是( )| A、6cm | B、5cm |
| C、3cm | D、2cm |
 如图,已知直角三角形ABC,∠C=90°.
如图,已知直角三角形ABC,∠C=90°.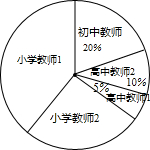 萧山区2014教师招聘有拉开序幕,这给很多有志于教育事业的人员很多机会.下面是今年报考人数统计表(数学)
萧山区2014教师招聘有拉开序幕,这给很多有志于教育事业的人员很多机会.下面是今年报考人数统计表(数学)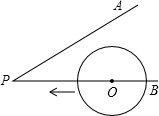 如图,∠APB=30°,点O是射线PB上的一点,OP=5cm,若以点O为圆心,半径为1.5cm的⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的距离为
如图,∠APB=30°,点O是射线PB上的一点,OP=5cm,若以点O为圆心,半径为1.5cm的⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的距离为 如图,在等腰△ABC的两腰AB、BC上分别取点D和E,使DB=DE,此时恰有∠ADE=
如图,在等腰△ABC的两腰AB、BC上分别取点D和E,使DB=DE,此时恰有∠ADE=