题目内容
3．
如图的直角三角形中未知边的长x等于（ ）| A． | 5 | B． | $\sqrt{5}$ | C． | 13 | D． | $\sqrt{13}$ |
分析 在直角三角形中，由勾股定理求出斜边x即可．
解答 解：由勾股定理得：x=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$；
故选：D．
点评 本题考查了勾股定理；熟练掌握勾股定理，在直角三角形中，已知两条直角边长，由勾股定理即可求出斜边的长．
练习册系列答案
相关题目
11．下列计算正确的是（ ）
| A． | $\sqrt{4}$-$\sqrt{3}$=1 | B． | $\sqrt{2}$×$\sqrt{\frac{1}{2}}$=1 | C． | $\sqrt{6}$÷$\sqrt{2}$=2 | D． | $\sqrt{8}$=±2$\sqrt{2}$ |
如图，平面直角坐标系中，△OAB的顶点A的坐标为（3，-2），点B在y轴负半轴上，若OA=AB，则点B的坐标为（0，-4）．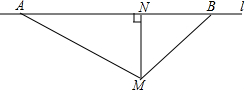
根据道路交通管理条例的规定，在某段笔直的公路l上行驶的车辆，限速60千米/时．已知测速点M到测速区间的端点A，B的距离分别为50米、34米，M距公路l的距离（即MN的长）为30米．现测得一辆汽车从A到B所用的时间为5秒，通过计算判断此车是否超速．
12．下面命题中，假命题是（ ）
| A． | 有一个角是100°的两个等腰三角形相似 | |
| B． | 全等三角形都是相似三角形 | |
| C． | 两边对应成比例，且有一个角相等的两个三角形相似 | |
| D． | 两条直角边对应成比例的两个直角三角形相似 |
如图所示，M是AC的中点，N是BC的中点，若AM=1cm，BN=1.5cm．求AB的长．