题目内容
用配方法求:
(1)y=-x2-2x+5
(2)y=3x2+2x-1.
(1)y=-x2-2x+5
(2)y=3x2+2x-1.
考点:二次函数的三种形式
专题:
分析:(1)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式;
(2)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
(2)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
解答:解:(1)y=-x2-2x+5=-(x2+2x+1)+1+5=-(x+1)2+6;
(2)y=3x2+2x-1=3(x2+
x+
)-
-1=3(x+
)2-
.
(2)y=3x2+2x-1=3(x2+
| 2 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题考查了二次函数的解析式有三种形式:
(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);
(2)顶点式:y=a(x-h)2+k;
(3)交点式(与x轴):y=a(x-x1)(x-x2).
(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);
(2)顶点式:y=a(x-h)2+k;
(3)交点式(与x轴):y=a(x-x1)(x-x2).

练习册系列答案
相关题目
 有理数a,b在数轴上的对应点的位置如图所示,则( )
有理数a,b在数轴上的对应点的位置如图所示,则( )| A、a+b=0 |
| B、a+b>0 |
| C、a-b<0 |
| D、a-b>0 |
 PA,PB切⊙O于点A、B,CD切⊙O于点E.
PA,PB切⊙O于点A、B,CD切⊙O于点E. 如图是一个长方体纸盒的展开图,在展开图的每个面上都标有数字,请根据要求回答问题:
如图是一个长方体纸盒的展开图,在展开图的每个面上都标有数字,请根据要求回答问题: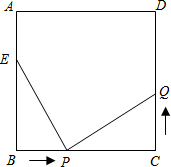 如图,已知正方形ABCD的边长为10cm,点E在边AB上,且AE=4cm,
如图,已知正方形ABCD的边长为10cm,点E在边AB上,且AE=4cm,