题目内容
18.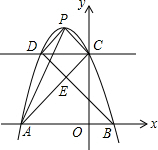 已知抛物线y=ax2+bx+c(a≠0)经过点A(-3,0),B(1,0),C(0,3)三点.
已知抛物线y=ax2+bx+c(a≠0)经过点A(-3,0),B(1,0),C(0,3)三点.(1)求该抛物线的解析式及顶点P的坐标;
(2)连接PA、AC、CP,求△PAC的面积;
(3)过点C作y轴的垂线,交抛物线于点D,连接PD、BD,BD交AC于点E,判断四边形PCED的形状,并说明理由.
分析 (1)根据待定系数法将A(-3,0),B(1,0),C(0,3)三点代入解析式求出即可,再利用配方法求出顶点坐标;
(2)利用两点之间距离公式求出PA=2$\sqrt{5}$,PC=$\sqrt{2}$,AC=3$\sqrt{2}$,进而得出△PAC为直角三角形,求出面积即可;
(3)首先求出点D的坐标为(-2,3),PC=DP,进而得出四边形PCED是菱形,再利用∠PCA=90°,得出答案即可.
解答 解:(1)由题意得:$\left\{\begin{array}{l}{9a-3b+c=0}\\{a+b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$,
∴该抛物线的解析式为:y=-x2-2x+3=-(x+1)2+4,
故P(-1,4); (2)∵y=-x2-2x+3=-(x+1)2+4,
(2)∵y=-x2-2x+3=-(x+1)2+4,
∴P(-1,4),
∵A(-3,0),B(1,0),C(0,3),
∴PA=2$\sqrt{5}$,PC=$\sqrt{2}$,AC=3$\sqrt{2}$,
∵PA2=PC2+AC2,
∴∠PCA=90°,
∴S△APC=$\frac{1}{2}$AC•PC=$\frac{1}{2}$×$\sqrt{2}$×3$\sqrt{2}$=3;
(3)四边形PCED是正方形,
理由:∵点C与点D关于抛物线的对称轴对称,点P为抛物线的顶点,
∴点D的坐标为(-2,3),PC=DP,
∵A(-3,0),C(0,3),代入y=kx+b,
$\left\{\begin{array}{l}{b=3}\\{-3k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
∴直线AC的函数关系式是:y=x+3,
同理可得出:直线DP的函数关系式是:y=x+5,
∴AC∥DP,
同理可得:PC∥BD,
∴四边形PCED是菱形,
又∵∠PCA=90°,
∴四边形PCED是正方形.
点评 此题考查了二次函数解析式的确定、函数图象交点坐标的求法以及菱形与正方形的判定方法等知识,正确掌握正方形的判定方法是解题关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 在地球上,上抛的篮球一定会下落,是必然事件 | |
| B. | 买一张福利彩票一定中奖,是不可能事件 | |
| C. | 抛掷一个正方体骰子,点数为奇数的概率是$\frac{1}{3}$ | |
| D. | 从一个装有5个黑球和1个红球的口袋中,摸出一个球是黑球是必然事件 |
| A. | -40=1 | B. | 2a(a+1)=2a2+2a | C. | (a+b)-1=a-1+b-1 | D. | (y-2x)(y+2x)=y2-2x2 |
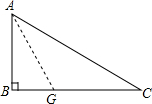 如图,已知直角△ABC中,∠B=90°,AB=6cm,BC=8cm,把AB沿AG折叠,使B点恰好落在AC上,求折痕AG的长.
如图,已知直角△ABC中,∠B=90°,AB=6cm,BC=8cm,把AB沿AG折叠,使B点恰好落在AC上,求折痕AG的长. 如图,已知抛物线y=ax2+bx-5(a≠0)与x轴交于点A(1,0)及点B,对称轴为直线x=3.
如图,已知抛物线y=ax2+bx-5(a≠0)与x轴交于点A(1,0)及点B,对称轴为直线x=3.