题目内容
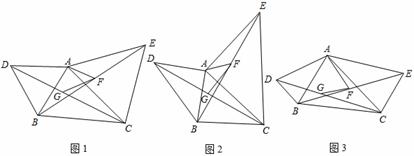
已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE;∠DAB=∠CAE,连接DC与BE,G、F分别是DC与BE的中点.
(1)探索发现:
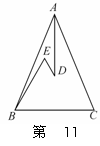
如图1,若∠DAB=60°,则∠AFG= ; 如图2,若∠DAB=90°,则∠AFG= ;
(2)探究证明:如图3,若∠DAB=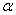 ,试探究∠AFG与
,试探究∠AFG与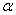 的数量关系?并给予证明;
的数量关系?并给予证明;
(3)动手实践:
如果∠ACB为锐角,AB≠AC,∠BAC≠90°,点M在线段BC上运动,连接AM,以AM为一边,以点A为直角顶点,且在AM的右侧作等腰直角△AMN,连接NC;试探究:若NC⊥BC(点C、M重合除外),则∠ACB等于多少度?请同学们自己动手画出相应图形,并说明理由.(画图不写作法)
解:(1)60°,45°;
(2)解:连接AG
 ∵∠DAB=∠CAE,∴∠DAC=∠BAE.
∵∠DAB=∠CAE,∴∠DAC=∠BAE.
又AD=AB,AC=AE,
∴△ADC≌△ABE(SAS)
∴∠1=∠2.
又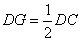 ,
,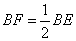 ,于是DG=BF.且AD=AB,
,于是DG=BF.且AD=AB,
∴△ADG≌△ABF(SAS)
∴AG=AF且∠DAG=∠BAF,于是易得∠GAF=∠DAB=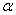 .
.
也就是说△AGF为顶角为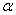 的等腰三角形,
的等腰三角形,
∴∠AFG=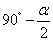 .
.
(3)简易画图步骤:1.先画等腰直角三角形AMN;
2.找个点C,使得CM⊥CN;
3.在CM延长线上任取一点B,连接AB,AC.(作图不计分)
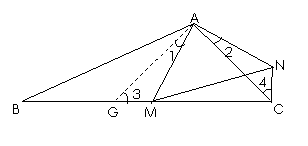
解:过点A作AC的垂线交BC于点G
由于∠1与∠2均与∠MAC互余,∴∠1=∠2.
由于∠3与∠4均与∠ACM互余,∴∠3=∠4.
又AM=AN,∴△AMG≌△ANC(AAS).
∴AG=AC.又AG⊥AC,
∴△AGC为等腰直角三角形.
∴∠ACB=∠ACG=45°.

练习册系列答案
相关题目

 ,其中 x =-2,y =
,其中 x =-2,y = .
.
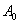 ,
, ,
,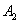 ,
,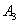 ,
,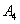 ,
, .现有甲乙两人同时从
.现有甲乙两人同时从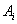 (i=1,2,3,4,5)下车是等可能的.
(i=1,2,3,4,5)下车是等可能的. 无意义.
无意义. ,1.2,
,1.2, ,0,-(-2),(-1)2011中,负数的个数有 ( )
,0,-(-2),(-1)2011中,负数的个数有 ( )