题目内容

7．（1）$-{3^2}+\sqrt{\frac{1}{4}}×{2^3}+{（{\frac{1}{5}}）^{-1}}$；       
（2）化简：$\frac{x^2}{x-1}+\frac{1}{1-x}$．

分析 （1）原式利用乘方的意义，负整数指数幂法则，以及算术平方根定义计算即可得到结果；
（2）原式变形后，利用同分母分式的减法法则计算，约分即可得到结果．

解答 解：（1）原式=-9+$\frac{1}{2}$×8+5=-9+4+5=0；
（2）原式=$\frac{{x}^{2}}{x-1}$-$\frac{1}{x-1}$=$\frac{（x+1）（x-1）}{x-1}$=x+1．

点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
17．先化简$\frac{1+x}{{{x^2}+x-2}}÷（x-2+\frac{3}{x+2}）$，再选一个你喜欢的数代入求值．
18．菱形ABCD中，两条对角线AC，BD相交于点O，点E和点F分别是BC和CD上一动点，且∠EOF+∠BCD=180°，连接EF．

（1）如图1，当∠ABC=90°时，若AC=4$\sqrt{2}$，BE=$\frac{3}{2}$，求线段EF的长；
（2）如图2，当∠ABC=60°时，求证：CE+CF=$\frac{1}{2}$AB；
（3）如图3，当∠ABC=90°时，将∠EOF的顶点移到AO上任意一点O′处，∠EO′F绕点O′旋转，仍满足∠EO′F+∠BCD=180°，O′E交BC的延长线一点E，射线O′F交CD的延长线上一点F，连接EF．探究在整个运动变化过程中，线段CE、CF，O′C之间满足的数量关系，并证明你的结论．
15．如图2，在平面直角坐标系xOy中，已知OP平分∠yOx．点P（2，2），点A在x轴正半轴上，联结PA，过点P作PB⊥PA交轴正半轴于点B．
（1）如图1，当PA⊥x轴时，求点A的坐标；
（2）如图2，当PA不垂直于x轴时，联结AB，试判断△PAB的形状，并说明理由；
（3）如图2，当PA不垂直于x轴时，请直接写出四边形APBO的面积．
2．从1，3，-4这三个数中，随机抽取两个数相乘，积是正数的概率是（　　）
A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{2}{3}$D．$\frac{3}{4}$
12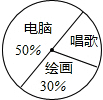．如图是八年级（2）班参加课外兴趣小组人数的扇形统计图，则表示唱歌兴趣小组人数的扇形的圆心角度数为（　　）
A．36°B．72°C．108°D．180°
19．如图是某市某中学八年级（1）班学生参加音乐、美术、体育课外兴趣小组人数的部分条形统计图和扇形统计图，则下列说法错误的是（　　）
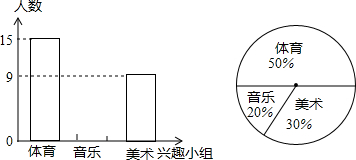
A．八年级（1）班参加这三个课外兴趣小组的学生总人数为30人
B．在扇形统计图中，八年级（1）班参加音乐兴趣小组的学生人数所占的圆心角度数为82°
C．八年级（1）班参加音乐兴趣小组的学生人数为6人
D．若该校八年级参加这三个兴趣小组的学生共有200人，那么估计全年级参加美术兴趣小组的学生约有60人
16．已知点P1（-4，3）和P2（-4，-3），则P1和P2（　　）
A．关于原点对称B．关于y轴对称C．关于x轴对称D．不存在对称关系
17．某工程队准备修建一条长1200米的道路，由于采用新的施工方式，实际每天修建道路的速度比原计划快20%，结果提前两天完成任务，若设原计划每天修建道路x米，则根据题意可列方程为（　　）
A．$\frac{1200}{x}$-$\frac{1200}{（1+20%）x}$=2B．$\frac{1200}{（1-20%）x}$-$\frac{1200}{x}$=2
C．$\frac{1200}{（1+20%）x}$-$\frac{1200}{x}$=2D．$\frac{1200}{x}$-$\frac{1200}{（1-20%）x}$=2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网