Question

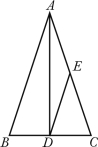
（本题满分8分）如图，等腰△ABC中，AB=AC, BC=10,角平分线AD=12,点E是AC中点，求DE的长．

Answer 1

．

【解析】

试题分析：由等腰三角形的性质得AD⊥BC,且DC=BC=5，在Rt△ACD中，由勾股定理得：AC=13，再利用直角三角形的中点的性质得DE的长．

试题解析：【解析】
∵AB=AC ，AD 是角平分线，

∴AD⊥BC,且DC=BC=5，

∵AD=12，

∴在Rt△ACD中，由勾股定理得：AC=，

∵点E是AC中点，

∴DE=AC= ．

考点：等腰三角形的性质；勾股定理；直角三角形的中线的性质．