题目内容
如图①,美丽的弦图,蕴含着四个全等的直角三角形.
(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为 ,较短的直角边为
,较短的直角边为 ,斜边长为
,斜边长为 ,试利用图①验证勾股定理;
,试利用图①验证勾股定理;
(2)如图②,将这四个全等的直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(实线)的周长为 ,
, 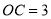 ,求该飞镖状图案的面积;
,求该飞镖状图案的面积;
(3)如图③,将八个全等的直角三角形紧密地拼接,记图中正方形 ,正方形
,正方形 ,正方形
,正方形 的面积分别为
的面积分别为 ,
,  ,
,  ,若
,若 ,则
,则 =________.
=________.



练习册系列答案
相关题目


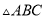 中,
中, 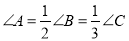 ,则它的三条边之比为( ).
,则它的三条边之比为( ).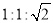 B.
B. 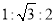 C.
C.  D.
D. 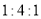
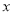 +b的图象经过第一、二、四象限,则在平面直角系数中二次函数y=a
+b的图象经过第一、二、四象限,则在平面直角系数中二次函数y=a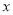 2+b
2+b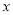 的图象大致是 ( )
的图象大致是 ( )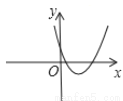 B.
B. 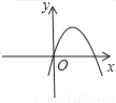 C.
C. 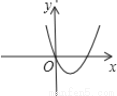 D.
D. 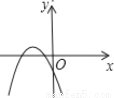
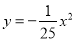 ,当水面离桥拱顶的高度DO是4m时,这时水面宽度AB为( )
,当水面离桥拱顶的高度DO是4m时,这时水面宽度AB为( )