题目内容
10.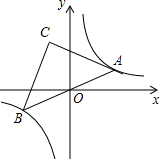 如图,点A是双曲线y=$\frac{4}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
如图,点A是双曲线y=$\frac{4}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )| A. | y=-$\frac{1}{4}$x | B. | y=-$\frac{1}{2}$x | C. | y=-$\frac{4}{x}$ | D. | y=-$\frac{2}{x}$ |
分析 根据题意做出合适的辅助线,然后证明三角形全等,设出点C的坐标,从而可以得到点C所在函数的解析式,本题得以解决.
解答  解:作AD⊥x轴与点D,连接OC,作CE⊥y轴于点E,
解:作AD⊥x轴与点D,连接OC,作CE⊥y轴于点E,
∵△ABC为等腰直角三角形,点O时AO的中点,
∴OC=OA,CO⊥AO,
∴∠COE=∠AOD,
∵∠OEC=∠ODA=90°,
∴△OEC≌△ODA(AAS),
∴OD=OE,AD=CE,
设点C的坐标为(x,y),则点A为(-y,x),
∵点A是双曲线y=$\frac{4}{x}$上,
∴-yx=4,
∴xy=-4,
∴点C所在的函数解析式为:y=$\frac{-4}{x}$,
故选C.
点评 本题考查反比例函数图象上点的坐标特征,等腰直角三角形、轨迹,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
1.计算$\sqrt{(-4)^{2}}$的结果是( )
| A. | 4 | B. | ±4 | C. | 2 | D. | -4 |
18.若$\sqrt{a+b+5}$+|2a-b+1|=0,则(b-a)2016的值为( )
| A. | 1 | B. | -1 | C. | 52016 | D. | -52016 |
5.点P(1,2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.如果等腰梯形的三边长为3、4、11,那么这个等腰梯形的周长是( )
| A. | 29 | B. | 21或29 | C. | 21或22 | D. | 21、22或29 |
2.下列命题是真命题的是( )
| A. | 如果a2=b2,则a=b | |
| B. | 两边一角对应相等的两个三角形全等 | |
| C. | $\sqrt{81}$的算术平方根是9 | |
| D. | x=2 y=1是方程2x-y=3的解 |

 如图所示,点A的坐标为(2,3),将点A绕原点O顺时针旋转90°后得到点A',则A′的坐标为(3,-2).
如图所示,点A的坐标为(2,3),将点A绕原点O顺时针旋转90°后得到点A',则A′的坐标为(3,-2).