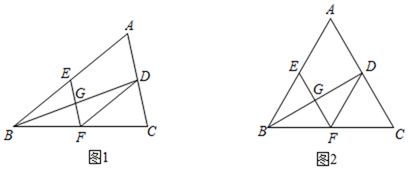Question

【题目】阅读与计算，请阅读以下材料，并完成相应的问题．

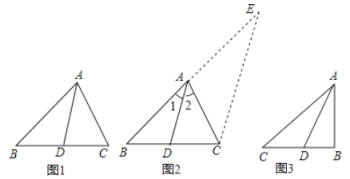
角平分线分线段成比例定理，如图1，在△ABC中，AD平分∠BAC，则＝．下面是这个定理的部分证明过程．

证明：如图2，过C作CE∥DA．交BA的延长线于E．…

任务：（1）请按照上面的证明思路，写出该证明的剩余部分；

（2）填空：如图3，已知Rt△ABC中，AB＝3，BC＝4，∠ABC＝90°，AD平分∠BAC，则△ABD的周长是　 　．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）过C作CE∥DA．交BA的延长线于E，利用平行线分线段成比例定理得到＝，利用平行线的性质得∠2=∠ACE，∠1=∠E，由∠1=∠2得∠ACE=∠E，所以AE=AC，于是有＝；
（2）先利用勾股定理计算出AC=5，再利用（1）中的结论得到＝，即＝，则可计算出BD=，然后利用勾股定理计算出AD=，从而可得到△ABD的周长．

（1）过C作CE∥DA．交BA的延长线于E，

∵CE∥AD，

∴＝，∠2＝∠ACE，∠1＝∠E，

∵AD平分∠BAC

∴∠1＝∠2，

∴∠ACE＝∠E，

∴AE＝AC，

∴＝；

（2）∵AB＝3，BC＝4，∠ABC＝90°，

∴AC＝5，

∵AD平分∠BAC，

∴＝，即＝，

∴BD＝，

∴AD＝＝＝，

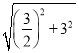∴△ABD的周长＝+3+＝．

故答案为：．