题目内容
15.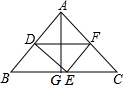 如图,点D,E,F分别是△ABC的边AB,BC,AC的中点,若BC上的高是AG的长为6cm,四边形ADEF的面积为12cm,求BC的长.
如图,点D,E,F分别是△ABC的边AB,BC,AC的中点,若BC上的高是AG的长为6cm,四边形ADEF的面积为12cm,求BC的长.
分析 利用三角形中位线定理和三角形的面积公式得到S△ADF=S△DFE=S△DBE=S△EFC,则易求△ABC的面积,由此再来求BC的长度.
解答  解:∵点D、F是AB、AC的中点,
解:∵点D、F是AB、AC的中点,
∴DF是△ABC的中位线,
∴DF∥BC,DF=$\frac{1}{2}$BC.
∴点A到边DF的距离和点E到边DF的距离相等,
又∵点E是BC边上的中点,
∴BE=EC=$\frac{1}{2}$BC,
∴DF=BE=EC,
∴S△DFE=S△DBE=S△EFC,
∴S△ADF=S△DFE=S△DBE=S△EFC,
∵四边形ADEF的面积为12cm,
∴S△ABC=2S四边形ADEF=24(cm2),
又BC上的高是AG的长为6cm,
∴$\frac{1}{2}$BC•AG=$\frac{1}{2}$BC×6=24,
则BC=8cm.
点评 本题考查了三角形中位线定理和三角形的面积.根据题意推知S△ADF=S△DFE=S△DBE=S△EFC是解题的难点.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
6.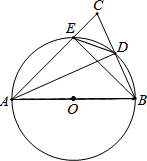 如图,在△ABC中,∠BAC=45°,以AB为直径的圆分别交BC,AC于D,E两点,AD交BE于F点,现给出下列命题:①$\sqrt{2}$DE+BD=AD;②△ABE与△ABD的面积差为$\frac{1}{2}$ED2,则( )
如图,在△ABC中,∠BAC=45°,以AB为直径的圆分别交BC,AC于D,E两点,AD交BE于F点,现给出下列命题:①$\sqrt{2}$DE+BD=AD;②△ABE与△ABD的面积差为$\frac{1}{2}$ED2,则( )
 如图,在△ABC中,∠BAC=45°,以AB为直径的圆分别交BC,AC于D,E两点,AD交BE于F点,现给出下列命题:①$\sqrt{2}$DE+BD=AD;②△ABE与△ABD的面积差为$\frac{1}{2}$ED2,则( )
如图,在△ABC中,∠BAC=45°,以AB为直径的圆分别交BC,AC于D,E两点,AD交BE于F点,现给出下列命题:①$\sqrt{2}$DE+BD=AD;②△ABE与△ABD的面积差为$\frac{1}{2}$ED2,则( )| A. | ①是假命题,②是真命题 | B. | ①是真命题,②是假命题 | ||
| C. | ①是假命题,②是假命题 | D. | ①是真命题,②是真命题 |
 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2,其中正确的序号是①③④.
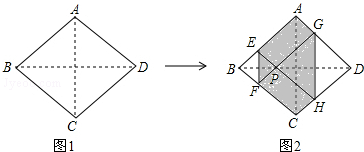
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2,其中正确的序号是①③④. 把一张长方形纸条按如图所示折叠.求证:∠HBC=∠HCB.
把一张长方形纸条按如图所示折叠.求证:∠HBC=∠HCB.