题目内容
5. 已知:如图,在△ABC中,AB=AC,D是BC上一动点,E,F分别在AB,AC上,且BE=CD,
已知:如图,在△ABC中,AB=AC,D是BC上一动点,E,F分别在AB,AC上,且BE=CD,BD=CF,求证:∠EDF=∠B.
分析 由等腰三角形的性质得出∠B=∠C,由SAS证明△BED≌△CDF,得出对应角相等BED=∠CDF,再由三角形的外角性质即可得出结论.
解答 证明:∵AB=AC,
∴∠B=∠C,
在△BED和△CDF中,$\left\{\begin{array}{l}{BE=CD}&{\;}\\{∠B=∠C}&{\;}\\{BD=CF}&{\;}\end{array}\right.$,
∴△BED≌△CDF(SAS),
∴∠BED=∠CDF,
∵∠EDC=∠BED+∠B,∠EDC=∠EDF+∠CDF,
∴∠EDF=∠B.
点评 本题考查了等腰三角形的性质、全等三角形的判定与性质、三角形的外角性质;熟练掌握等腰三角形的性质,证明三角形全等得出对应角相等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图,坡面AB的坡度为1:3,且AB=10米,则斜坡的水平宽度AC的长为( )
如图,坡面AB的坡度为1:3,且AB=10米,则斜坡的水平宽度AC的长为( )
 如图,坡面AB的坡度为1:3,且AB=10米,则斜坡的水平宽度AC的长为( )
如图,坡面AB的坡度为1:3,且AB=10米,则斜坡的水平宽度AC的长为( )| A. | 3$\sqrt{10}$米 | B. | $\sqrt{10}$米 | C. | 2$\sqrt{10}$米 | D. | 4$\sqrt{10}$米 |
17.某商店一套服装进价为300元,如果按标价的八折销售可获利80元,那么该服装的标价是( )
| A. | 375元 | B. | 380元 | C. | 450元 | D. | 475元 |
 如图,△ABC中,BO、CO分别平分∠ABC和∠ACB.
如图,△ABC中,BO、CO分别平分∠ABC和∠ACB. 如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°求证:AG=FG.
如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°求证:AG=FG.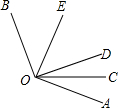 如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.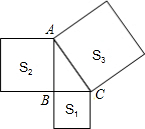 如图,在△ABC中,∠ABC=90°,分别以BC,AB,AC为边向外作正方形,面积分别记为S1、S2、S3,若S2=4,S3=6,则S1=( )
如图,在△ABC中,∠ABC=90°,分别以BC,AB,AC为边向外作正方形,面积分别记为S1、S2、S3,若S2=4,S3=6,则S1=( )