题目内容
反比例函数y1= 图象上的一些点的坐标如下表所示:
图象上的一些点的坐标如下表所示:
| x | … | -3 | -2 | -1 | … | 1 | 2 | 3 | … |
| y | … | 2 | 3 | 6 | … | -6 | -3 | -2 | … |
(2)一次函数的表达式是y2=mx-1(其中,m是常数,且m≠0).
①求证:不论m为何值,该一次函数的图象都经过一个定点;
②已知一次函数的图象与反比例函数图象交于点(-6,1)和点(3,-2),请你直接写出使式子
 >mx-1成立的x的取值范围.
>mx-1成立的x的取值范围.
(1)解:把(-3,2)代入y1= 得:2=
得:2= ,
,
解得:k=-6,
∴y1=- ,
,
故答案为:y1=- ;
;
(2)①证明:把x=0代入y2=mx-1,得y2=-1,
∴不论m为何值,该一次函数的图象都经过定点(0,-1);
②解:如图:
根据图象可知:使式子 >mx-1成立的x的取值范围是-6<x<0或x>3.
>mx-1成立的x的取值范围是-6<x<0或x>3.
分析:(1)从表中取点(-3,2)代入y1= ,求出k即可;
,求出k即可;
(2)①把x=0代入y2=mx-1求出y2=-1,即可得出过定点(0,-1);②画出函数的草图,根据图象和函数的性质即可得出答案.
点评:本题考查了用待定系数法求反比例函数的解析式和一次函数与反比例函数的交点问题,主要考查学生的计算能力,用了数形结合思想.
 得:2=
得:2= ,
,解得:k=-6,
∴y1=-
 ,
,故答案为:y1=-
 ;
;(2)①证明:把x=0代入y2=mx-1,得y2=-1,
∴不论m为何值,该一次函数的图象都经过定点(0,-1);
②解:如图:

根据图象可知:使式子
 >mx-1成立的x的取值范围是-6<x<0或x>3.
>mx-1成立的x的取值范围是-6<x<0或x>3.分析:(1)从表中取点(-3,2)代入y1=
 ,求出k即可;
,求出k即可;(2)①把x=0代入y2=mx-1求出y2=-1,即可得出过定点(0,-1);②画出函数的草图,根据图象和函数的性质即可得出答案.
点评:本题考查了用待定系数法求反比例函数的解析式和一次函数与反比例函数的交点问题,主要考查学生的计算能力,用了数形结合思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
反比例函数y1=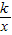 图象上的一些点的坐标如下表所示:
图象上的一些点的坐标如下表所示:
(1)这个反比例函数的表达式是______;
(2)一次函数的表达式是y2=mx-1(其中,m是常数,且m≠0).
①求证:不论m为何值,该一次函数的图象都经过一个定点;
②已知一次函数的图象与反比例函数图象交于点(-6,1)和点(3,-2),请你直接写出使式子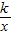 >mx-1成立的x的取值范围.
>mx-1成立的x的取值范围.
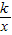 图象上的一些点的坐标如下表所示:
图象上的一些点的坐标如下表所示:| x | … | -3 | -2 | -1 | … | 1 | 2 | 3 | … |
| y | … | 2 | 3 | 6 | … | -6 | -3 | -2 | … |
(2)一次函数的表达式是y2=mx-1(其中,m是常数,且m≠0).
①求证:不论m为何值,该一次函数的图象都经过一个定点;
②已知一次函数的图象与反比例函数图象交于点(-6,1)和点(3,-2),请你直接写出使式子
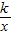 >mx-1成立的x的取值范围.
>mx-1成立的x的取值范围. 已知二次函数y1=x2-2x-1的图象和反比例函数
已知二次函数y1=x2-2x-1的图象和反比例函数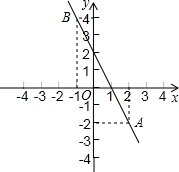 已知直线y1=-2x+2上有两点A(2,-2),B(-1,4).
已知直线y1=-2x+2上有两点A(2,-2),B(-1,4).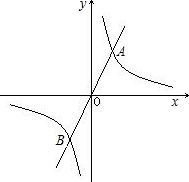 为(1,2).
为(1,2).