题目内容
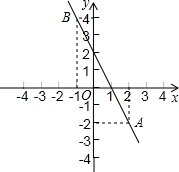 已知直线y1=-2x+2上有两点A(2,-2),B(-1,4).
已知直线y1=-2x+2上有两点A(2,-2),B(-1,4).(1)请说明存在一个反比例函数y2=
| k | x |
(2)用描点法在右图中画出该反比例函数的图象,并根据图象判断,当x取何值时,y1>y2.
分析:(1)把A的坐标代入反比例函数的解析式求出k即可;
(2)求出图象上点的坐标,在平面直角坐标系中描出,连接即可;根据图象的特点即可求出答案.
(2)求出图象上点的坐标,在平面直角坐标系中描出,连接即可;根据图象的特点即可求出答案.
解答: 解:(1)把A(2,-2)代入y2=
解:(1)把A(2,-2)代入y2=
,
得:-2=
,
∴k=-4,
∴y2=-
,
答:这个函数的解析式是y2=-
.
(2)如图所示:
从图象可知:当x<-1或0<x<2时,y1>y2.
 解:(1)把A(2,-2)代入y2=
解:(1)把A(2,-2)代入y2=| k |
| x |
得:-2=
| k |
| 2 |
∴k=-4,
∴y2=-
| 4 |
| x |
答:这个函数的解析式是y2=-
| 4 |
| x |
(2)如图所示:
从图象可知:当x<-1或0<x<2时,y1>y2.
点评:本题主要考查对用待定系数法求反比例函数的解析式,反比例函数与一次函数的交点问题,反比例函数的图象等知识点的理解和掌握,能正确画出图象和根据图象得到结论(当x<-1或0<x<2时,y1>y2.)是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
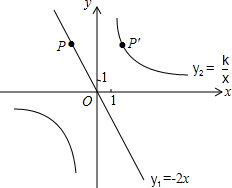 如图,已知直线y1=-2x经过点P(-2,a),点P关于y轴的对称点P′在反比例函数y2=
如图,已知直线y1=-2x经过点P(-2,a),点P关于y轴的对称点P′在反比例函数y2=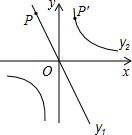 如图,已知直线y1=-2x经过点P(-2,a),点P关于y轴的对称点P′在反比例函数
如图,已知直线y1=-2x经过点P(-2,a),点P关于y轴的对称点P′在反比例函数